



Next: Effective screening medium method
Up: User's manual of OpenMX
Previous: Automatic running test of
Contents
Index
A numerically exact low-order scaling method is supported for large-scale calculations [80].
The computational effort of the method scales as O(
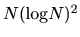 ), O(
), O(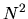 ), and O(
), and O(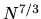 )
for one, two, and three dimensional systems, respectively, where
)
for one, two, and three dimensional systems, respectively, where 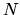 is the number of basis functions.
Unlike O(
is the number of basis functions.
Unlike O(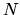 ) methods developed so far the approach is a numerically exact alternative to conventional
O(
) methods developed so far the approach is a numerically exact alternative to conventional
O(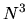 ) diagonalization schemes in spite of the low-order scaling, and can be applicable to
not only insulating but also metallic systems in a single framework. The well separated data
structure is suitable for the massively parallel computation as shown in Fig. 36.
However, the advantage of the method can be obtained
only when a large number of CPU cores are used for parallelization, since the prefactor of computational
efforts can be large. When you calculate low-dimensional large-scale systems using a large number of
CPU cores, the method can be a proper choice. To choose the method for diagonzalization, you can specify
the keyword 'scf.EigenvalueSolver' as
) diagonalization schemes in spite of the low-order scaling, and can be applicable to
not only insulating but also metallic systems in a single framework. The well separated data
structure is suitable for the massively parallel computation as shown in Fig. 36.
However, the advantage of the method can be obtained
only when a large number of CPU cores are used for parallelization, since the prefactor of computational
efforts can be large. When you calculate low-dimensional large-scale systems using a large number of
CPU cores, the method can be a proper choice. To choose the method for diagonzalization, you can specify
the keyword 'scf.EigenvalueSolver' as
scf.EigenvalueSolver cluster2
The method is supported only for colliear DFT calculations of cluster systems or periodic systems with
the 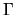 point for the Brillouin zone sampling.
As well as the total energy calculation, the force calculation by the low-order scaling method
is supported. Thus, it is possible to perform geometry optimization.
However, calculations of density of states and wave functions are not supported yet.
The number of poles in the contour integration [55] is controlled by a keyword:
point for the Brillouin zone sampling.
As well as the total energy calculation, the force calculation by the low-order scaling method
is supported. Thus, it is possible to perform geometry optimization.
However, calculations of density of states and wave functions are not supported yet.
The number of poles in the contour integration [55] is controlled by a keyword:
scf.Npoles.ON2 90
The number of poles to achieve convergence does not depend on the size of system [80],
but depends on the spectrum radius of system. If the electronic temperature more 300 K is used,
the use of 100 poles is enough to get sufficient convergence for the total energy and forces.
As an illustration, we show a calculation by the numerically exact low-order scaling method
using an input file 'C60_LO.dat' stored in the directorty 'work'.
% mpirun -np 8 openmx C60_LO.dat
As shown in Table 7, the total energy by the low-order scaling method
is equivalent to that by the conventional method within double precision, while
the computational time is much longer than that of the conventional method for such a
small system. We expect that the crossing point between the low-order scaling
and the conventional methods with respect to computational time is located at around 300 atoms
when using more than 100 cores for the parallel computation, although it depends on
the dimensionality of system.
Figure 36:
Speed-up ratio in the parallel computation of the diagonalization
in the SCF calculation for DNA by a hybrid scheme using MPI and OpenMP.
The speed-up ratio is defined by 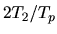 , where
, where 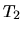 and
and 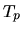 are the elapsed times obtained by two MPI processes and by
the corresponding number of processes and threads.
The parallel calculations were performed on a CRAY-XT5 machine consisting
of AMD opteron quad core processors (2.3 GHz).
The electric temperature of 700 K and 80 poles for the contour
integration are used. For comparison, the speed-up ratio for the parallel
computation of the conventional scheme using Householder and QR methods is
also shown for the case with a single thread. The elapsed time at cases
pointed by arrow is also shown for both the low-order scaling and
conventional methods.
are the elapsed times obtained by two MPI processes and by
the corresponding number of processes and threads.
The parallel calculations were performed on a CRAY-XT5 machine consisting
of AMD opteron quad core processors (2.3 GHz).
The electric temperature of 700 K and 80 poles for the contour
integration are used. For comparison, the speed-up ratio for the parallel
computation of the conventional scheme using Householder and QR methods is
also shown for the case with a single thread. The elapsed time at cases
pointed by arrow is also shown for both the low-order scaling and
conventional methods.
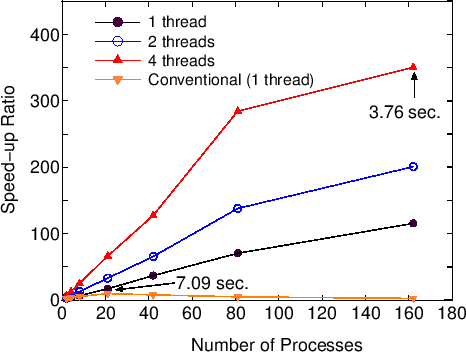 |
Table 7:
Total energy of a C60 molecule calculated by the numerically exact low-order scaling method
and conventional method, and its computational time (sec.) for the diagonalization using
8 processes in the MPI parallelization.
The input file is C60_LO.dat in the directory 'work'.
|
| Method |
Total energy (Hartree) |
Computational time (sec.) |
| Low-order |
-343.896238929370 |
69.759 |
| Conventional |
-343.896238929326 |
2.784 |
|




Next: Effective screening medium method
Up: User's manual of OpenMX
Previous: Automatic running test of
Contents
Index
t-ozaki
2013-05-22
![]() ), O(
), O(![]() ), and O(
), and O(![]() )
for one, two, and three dimensional systems, respectively, where
)
for one, two, and three dimensional systems, respectively, where ![]() is the number of basis functions.
Unlike O(
is the number of basis functions.
Unlike O(![]() ) methods developed so far the approach is a numerically exact alternative to conventional
O(
) methods developed so far the approach is a numerically exact alternative to conventional
O(![]() ) diagonalization schemes in spite of the low-order scaling, and can be applicable to
not only insulating but also metallic systems in a single framework. The well separated data
structure is suitable for the massively parallel computation as shown in Fig. 36.
However, the advantage of the method can be obtained
only when a large number of CPU cores are used for parallelization, since the prefactor of computational
efforts can be large. When you calculate low-dimensional large-scale systems using a large number of
CPU cores, the method can be a proper choice. To choose the method for diagonzalization, you can specify
the keyword 'scf.EigenvalueSolver' as
) diagonalization schemes in spite of the low-order scaling, and can be applicable to
not only insulating but also metallic systems in a single framework. The well separated data
structure is suitable for the massively parallel computation as shown in Fig. 36.
However, the advantage of the method can be obtained
only when a large number of CPU cores are used for parallelization, since the prefactor of computational
efforts can be large. When you calculate low-dimensional large-scale systems using a large number of
CPU cores, the method can be a proper choice. To choose the method for diagonzalization, you can specify
the keyword 'scf.EigenvalueSolver' as
