



Next: User definition of FNAN+SNAN
Up: Order(N) method
Previous: Divide-conquer method
Contents
Index
The DC method is robust and accurate for a wide variety of systems.
However, the size of truncated clusters to obtain an accurate result tends
to be large for metallic systems as shown in Fig. 16. A way of reducing
the computational efforts is to map the original vector space defined
by the truncated cluster into a Krylov subspace of which dimension
is smaller than that of the original space [30].
The Krylov subspace method is available by
scf.EigenvalueSolver Krylov
Basically, the accuracy and efficiency are controlled by the following
two keywords:
orderN.HoppingRanges 6.0
orderN.KrylovH.order 400
The keyword 'orderN.HoppingRanges'
defines the radius of a sphere centered on each atom in the same sense as
that in the DC method.
The dimension of the Krylov subspace of Hamiltonian in each truncated cluster
is given by 'orderN.KrylovH.order'.
Moreover, the Krylov subspace method can be precisely tuned by
the following keywords:
- orderN.Exact.Inverse.S on
 off, default=on
off, default=on
In case of 'orderN.Exact.Inverse.S=on',
the inverse of overlap
matrix for each truncated cluster is exactly evaluated.
Otherwise, see the next keyword 'orderN.KrylovS.order'.
- orderN.KrylovS.order 1200,
default=orderN.KrylovH.order
In case of 'orderN.Exact.Inverse.S=off',
the inverse is approximated
by a Krylov subspace method for the inverse, where the dimension of
the Krylov subspace of overlap matrix in each truncated cluster is
given by the keyword 'orderN.KrylovS.order'.
- orderN.Recalc.Buffer on
 off, default=on
off, default=on
In case of 'orderN.Recalc.Buffer=on', the buffer matrix is recalculated
at every SCF step. Otherwise, the buffer matrix is calculated at
the first SCF step, and fixed at the subsequent SCF steps.
- orderN.Expand.Core on
 off, default=on
off, default=on
In case of 'orderN.Expand.Core=on', the core region
is defined by atoms within a sphere with radius of
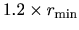 , where
, where
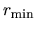 is the distance between the central atom and the nearest atom.
The core region defines a set of vectors used for the first step in the generation
of the Krylov subspace for each truncated cluster.
In case of 'orderN.Expand.Core=off', the central atom is considered
as the core region. The default is 'on'.
is the distance between the central atom and the nearest atom.
The core region defines a set of vectors used for the first step in the generation
of the Krylov subspace for each truncated cluster.
In case of 'orderN.Expand.Core=off', the central atom is considered
as the core region. The default is 'on'.
It is better to switch on 'orderN.Exact.Inverse.S'
and 'orderN.Expand.Core'
as the covalency increases, while the opposite could becomes better
in simple metallic systems.
In Fig. 17 the absolute error in the total energy calculated by the
Krylov and DC methods are shown for a wide variety of materials.
It is found that in comparison with the DC method, the Krylov subspace
method is more efficient especially for metallic systems,
and that the efficiency become comparable as the covalency
and ionicity in the electronic structure increase.
It is also noted that the O(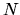 ) Krylov subspace method is well parallelized to realize
large-scale calculations.
The most efficient parallelization for the O(
) Krylov subspace method is well parallelized to realize
large-scale calculations.
The most efficient parallelization for the O(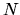 ) Krylov subspace method can be realized
by using the same number of MPI processes as that of atoms together with OpenMP threads.
Figure 18 shows that a system consisting of a hundred thousand
atoms can be treated on a massively parallel computer [31,32], where
the diamond structure consisting of 131072 carbon atoms is considered as a benchmark system.
) Krylov subspace method can be realized
by using the same number of MPI processes as that of atoms together with OpenMP threads.
Figure 18 shows that a system consisting of a hundred thousand
atoms can be treated on a massively parallel computer [31,32], where
the diamond structure consisting of 131072 carbon atoms is considered as a benchmark system.
Figure 17:
(a) absolute error, with respect to the band calculations,
in the total energy (Hartree/atom) calculated
by the Krylov subspace and DC methods for metals and finite
gap systems, (b) computational time (s/atom/MD).
For a substantial comparison, the calculations were
performed using a single Xeon processor.
The set of numbers in the parenthesis of (a) means the average
number of atoms in the core and buffer regions.
The set of numbers in the parenthesis of (b) means the
percentage of the dimension of the subspaces
relative to the total number of basis functions in the truncated
cluster, respectively.
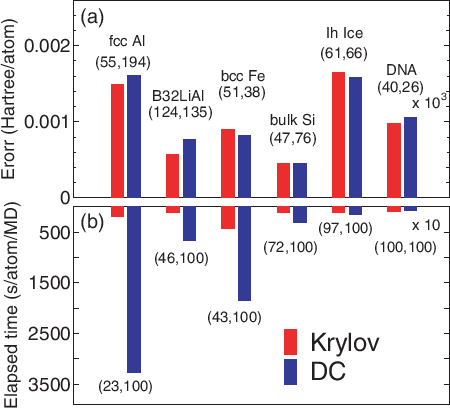 |
Figure 18:
Parallel efficiency of the O(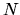 ) Krylov subspace method in the hybrid parallelization on the K-computer,
where eight threads were used for all the cases.
The diamond structure consisting of 131072 carbon atoms was considered as a benchmark system.
) Krylov subspace method in the hybrid parallelization on the K-computer,
where eight threads were used for all the cases.
The diamond structure consisting of 131072 carbon atoms was considered as a benchmark system.
 |




Next: User definition of FNAN+SNAN
Up: Order(N) method
Previous: Divide-conquer method
Contents
Index
t-ozaki
2013-05-22
![]() , where
, where
![]() is the distance between the central atom and the nearest atom.
The core region defines a set of vectors used for the first step in the generation
of the Krylov subspace for each truncated cluster.
In case of 'orderN.Expand.Core=off', the central atom is considered
as the core region. The default is 'on'.
is the distance between the central atom and the nearest atom.
The core region defines a set of vectors used for the first step in the generation
of the Krylov subspace for each truncated cluster.
In case of 'orderN.Expand.Core=off', the central atom is considered
as the core region. The default is 'on'.

