Next: On-the-fly control of SCF Up: SCF convergence Previous: General Contents Index
If the keyword 'scf.Kerker.factor' is not given in your input file,
OpenMX Ver. 3.8 automatically estimates a proper value of Kerker's factor ![]() by the following
equation:
by the following
equation:
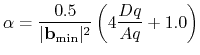 |
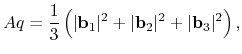 |
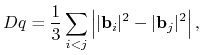 |