A couple of examples as benchmark calculations are shown below:
Si
The real part of dielectric function of Si bulk is shown for a series of k-grids in Fig. 81.
We see that as increasing k-grid from
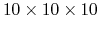 to
to
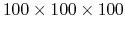 ,
the real part of dielectric function is getting converged.
It is found that we need to have a fine grid for the k-points to obtain a well converged result.
In Tables 14 and 15, we show the computational time and parallel efficiency
in the calculation of the conductivity and dielectric function for supercells of Si bulk.
The results suggest that it might be possible to treat systems including 1000 atoms if 1000 CPU cores are available.
,
the real part of dielectric function is getting converged.
It is found that we need to have a fine grid for the k-points to obtain a well converged result.
In Tables 14 and 15, we show the computational time and parallel efficiency
in the calculation of the conductivity and dielectric function for supercells of Si bulk.
The results suggest that it might be possible to treat systems including 1000 atoms if 1000 CPU cores are available.
Figure 81:
The dielectric function of Si crystal (primitive cell, 2 atoms) with 6 different K-grids:
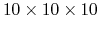 ,
,
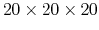 ,
,
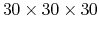 ,
,
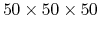 ,
,
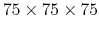 , and
, and
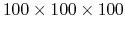 . The blue and red lines are real
and imaginary parts of dielectric function, respectively, where CDDF.FWHM=0.2 eV was used.
. The blue and red lines are real
and imaginary parts of dielectric function, respectively, where CDDF.FWHM=0.2 eV was used.
|
|
Table 14:
Computational time of conductivity and dielectric function of Si crystal.
| |
# of Si atoms |
Supercell |
Diagonalization |
k-Grid
|
| | Total time (s) |
|
| | (CPUs=128) |
|
|
| | Total time (s) |
|
| | (CPUs=256) |
|
|
| | Total time (s) |
|
| | (CPUs=512) |
|
|
| | Total time (s) |
|
| | (CPUs=1024) |
|
|
| | Total time (s) |
|
| | (CPUs=2048) |
|
|
|
| |
512 atoms |
4x4x4 |
Cluster |
1x1x1 |
3367.16826 |
1755.60797 |
919.21912 |
464.27761 |
253.32210 |
|
| |
|
4x4x4 |
ScaLAPACK |
2x1x1 |
6819.30193 |
3499.51872 |
1838.64406 |
948.87978 |
513.79250 |
|
| |
|
4x4x4 |
Band |
2x2x2 |
15300.58350 |
10217.17765 |
5953.19907 |
3518.84650 |
1747.20171 |
|
| |
1000 atoms |
5x5x5 |
Cluster |
1x1x1 |
|
|
6900.35370 |
3511.85143 |
1778.33693 |
|
| |
|
5x5x5 |
ScaLAPACK |
2x1x1 |
|
|
12994.17818 |
6817.43990 |
3460.76787 |
|
| |
|
5x5x5 |
Band |
2x2x2 |
|
|
43676.20392 |
26055.12739 |
13318.14587 |
|
Table 15:
Calculation time of conductivity and dielectric function of
Si crystal (512 atoms,
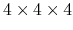 supercell, k-grid=
supercell, k-grid=
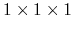 ).
The speed-up ratio with repect to the case with 128 CPU cores is shown in the last column.
).
The speed-up ratio with repect to the case with 128 CPU cores is shown in the last column.
| | |
|
|
|
| | |
|
|
|
| | |
|
|
|
| | |
|
|
|
| | |
|
|
|
| | |
|
|
|
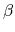 -PVDF
-PVDF
The real part of dielectric function of 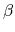 -PVDF (polyvinylidene fluoride) is shown for a series of k-grids
in Fig. 82. We see that the k-grid of
-PVDF (polyvinylidene fluoride) is shown for a series of k-grids
in Fig. 82. We see that the k-grid of
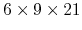 is required to get the convergent result.
In Tables 16 and 17, we show the computational time and parallel efficiency
in the calculation of the conductivity and dielectric function for supercells of
is required to get the convergent result.
In Tables 16 and 17, we show the computational time and parallel efficiency
in the calculation of the conductivity and dielectric function for supercells of 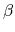 -PVDF.
It is confirmed that the parallel efficiency is reasonably good, and the elapsed time is less than one hour when
the CPU cores of 256 are used. In Fig. 83, we show the
-PVDF.
It is confirmed that the parallel efficiency is reasonably good, and the elapsed time is less than one hour when
the CPU cores of 256 are used. In Fig. 83, we show the 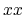 ,
, 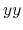 , and
, and 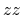 components of
real part of dielectric function of
components of
real part of dielectric function of 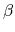 -PVDF for your reference.
-PVDF for your reference.
Figure 82:
The real part of dielectric function of 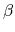 -PVDF (polyvinylidene fluoride) consisting of 6 atoms
in the
-PVDF (polyvinylidene fluoride) consisting of 6 atoms
in the
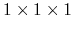 cell for a series of k-grids. CDDF.FWHM=0.2 eV was used.
cell for a series of k-grids. CDDF.FWHM=0.2 eV was used.
|
|
Table 16:
Total time of calculating conductivity and dielectric function of 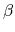 -PVDF (polyvinylidene fluoride)
consisting of 540 atoms which corresponds to the
-PVDF (polyvinylidene fluoride)
consisting of 540 atoms which corresponds to the
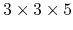 supercell.
supercell.
| | |
|
|
|
|
|
|
|
| | |
|
|
|
|
|
|
|
| | |
|
|
|
|
|
|
|
| | |
|
|
|
|
|
|
|
Table 17:
Calculation time of conductivity and dielectric function of 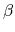 -PVDF (polyvinylidene fluoride)
consisting of 540 atoms which corresponds to the
-PVDF (polyvinylidene fluoride)
consisting of 540 atoms which corresponds to the
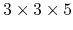 supercell, where k-grid of
supercell, where k-grid of
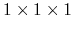 was used.
The speed-up ratio with repect to the case with 128 CPU cores is shown in the last column.
was used.
The speed-up ratio with repect to the case with 128 CPU cores is shown in the last column.
| | # of CPUs |
| | Total time of calculating |
|
| | conductivity and dielectric function (s) |
|
|
| | Ratio of |
|
| | total time by # of CPUs |
|
| | to total time by 128 CPUs |
|
|
|
| | 128 |
4215.67238 |
1.000 |
|
| | 256 |
2086.76841 |
2.020 |
|
| | 512 |
1061.06835 |
3.973 |
|
| | 1024 |
565.92209 |
7.449 |
|
| | 2048 |
329.42010 |
12.797 |
|
Figure 83:
The 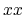 ,
, 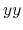 , and
, and 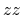 components of real parts of dielectric function of
components of real parts of dielectric function of 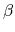 -PVDF (6 atoms,
-PVDF (6 atoms,
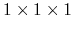 cell).
cell).
|
|
VO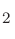 in the R phase
in the R phase
The real and imaginary parts of dielectric function of VO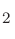 in the R phase are shown for a series of k-grids
in Fig. 84. We see that the k-grid of
in the R phase are shown for a series of k-grids
in Fig. 84. We see that the k-grid of
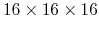 is required to get the convergent result.
Tables 18 and 19 show the computational time and parallel efficiency
in the calculation of the conductivity and dielectric function for supercells of VO
is required to get the convergent result.
Tables 18 and 19 show the computational time and parallel efficiency
in the calculation of the conductivity and dielectric function for supercells of VO in the R phase.
It is confirmed that the parallel efficiency is reasonably good, allowing us to treat large-scale systems
in an elapsed time of 1 hour.
in the R phase.
It is confirmed that the parallel efficiency is reasonably good, allowing us to treat large-scale systems
in an elapsed time of 1 hour.
Figure 84:
The real and imaginary parts of dielectric function of VO (R phase, 6 atoms,
(R phase, 6 atoms,
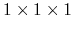 cell)
with a series of k-grids.
cell)
with a series of k-grids.
|
|
Table 18:
Calculation time of conductivity and dielectric function of VO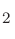 (R phase, 384 atoms,
(R phase, 384 atoms,
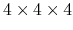 supercell)
supercell)
| | |
|
|
|
|
|
|
|
| | |
|
|
|
|
|
|
|
| | |
|
|
|
|
|
|
|
| | |
|
|
|
|
|
|
|
![]() to
to
![]() ,
the real part of dielectric function is getting converged.
It is found that we need to have a fine grid for the k-points to obtain a well converged result.
In Tables 14 and 15, we show the computational time and parallel efficiency
in the calculation of the conductivity and dielectric function for supercells of Si bulk.
The results suggest that it might be possible to treat systems including 1000 atoms if 1000 CPU cores are available.
,
the real part of dielectric function is getting converged.
It is found that we need to have a fine grid for the k-points to obtain a well converged result.
In Tables 14 and 15, we show the computational time and parallel efficiency
in the calculation of the conductivity and dielectric function for supercells of Si bulk.
The results suggest that it might be possible to treat systems including 1000 atoms if 1000 CPU cores are available.
![\includegraphics[width=17.0cm]{CDDF-Fig2.eps}](img594.png)
![]() -PVDF
-PVDF
![]() -PVDF (polyvinylidene fluoride) is shown for a series of k-grids
in Fig. 82. We see that the k-grid of
-PVDF (polyvinylidene fluoride) is shown for a series of k-grids
in Fig. 82. We see that the k-grid of
![]() is required to get the convergent result.
In Tables 16 and 17, we show the computational time and parallel efficiency
in the calculation of the conductivity and dielectric function for supercells of
is required to get the convergent result.
In Tables 16 and 17, we show the computational time and parallel efficiency
in the calculation of the conductivity and dielectric function for supercells of ![]() -PVDF.
It is confirmed that the parallel efficiency is reasonably good, and the elapsed time is less than one hour when
the CPU cores of 256 are used. In Fig. 83, we show the
-PVDF.
It is confirmed that the parallel efficiency is reasonably good, and the elapsed time is less than one hour when
the CPU cores of 256 are used. In Fig. 83, we show the ![]() ,
, ![]() , and
, and ![]() components of
real part of dielectric function of
components of
real part of dielectric function of ![]() -PVDF for your reference.
-PVDF for your reference.
![\includegraphics[width=14.0cm]{CDDF-Fig3.eps}](img596.png)
![]() in the R phase
in the R phase
![]() in the R phase are shown for a series of k-grids
in Fig. 84. We see that the k-grid of
in the R phase are shown for a series of k-grids
in Fig. 84. We see that the k-grid of
![]() is required to get the convergent result.
Tables 18 and 19 show the computational time and parallel efficiency
in the calculation of the conductivity and dielectric function for supercells of VO
is required to get the convergent result.
Tables 18 and 19 show the computational time and parallel efficiency
in the calculation of the conductivity and dielectric function for supercells of VO![]() in the R phase.
It is confirmed that the parallel efficiency is reasonably good, allowing us to treat large-scale systems
in an elapsed time of 1 hour.
in the R phase.
It is confirmed that the parallel efficiency is reasonably good, allowing us to treat large-scale systems
in an elapsed time of 1 hour.
![\includegraphics[width=17.0cm]{CDDF-Fig5.eps}](img599.png)