 Re: Relaxation of MoS2 ( No.1 ) |
- Date: 2014/02/13 22:21
- Name: T. Ozaki
- Hi,
The total energy at the last step is higher than that at the first step, which implies that you got
a local minimum. Perhaps, the optimization step at which the EF method starts to be employed is
a bit small. Since you didn't specify the keyword 'MD.Opt.StartDIIS', the default value of 5 was
used for your calculation. The use of larger value for that may change your result. Also, I wonder
that the SCF calculations converge at all the optimization steps. If not, the optimization process
is non-predictable.
I would comment a couple of things. It is known that the geometry optimization within the NC-DFT
method is much more difficult than the case of collinear DFT. Also, the relativistic effect in Mo
atom is not enough to change the geometrical structure largely. Thus, it would be better to perform
the geometry optimization within the collinear DFT. Once you got a convergent result within the
colinear DFT, you can switch from the collinear to NC-DFT scheme with spin-orbit coupling, and
calculate the band structure using the optimized structure. I guess that above the procedure can
provide an enough result for your purpose.
Also, I can notice a couple of improper specifications in your input file. First, the specification
of the basis functions is not a good choice.
The following
Mo Mo7.0-s2p2d1 Mo_CA13
S S7.0-s1p1d1 S_CA13
should be at least
Mo Mo7.0-s2p2d1 Mo_CA13
S S7.0-s2p2d1 S_CA13
or
Mo Mo7.0-s2p2d2 Mo_CA13
S S7.0-s2p2d2 S_CA13
to get a convergent result at certain level.
Second, the lattice vector of c-axis
<Atoms.UnitVectors
3.160 0.000 0.000
1.580 2.736640276 0.00
0.00000000 0.00000000 100.0
Atoms.UnitVectors>
may not be a good choice. I think that the vacuum of 20.0 (ang.) is enough to prevent interaction
between slabs. Also, if you really want to cut the spurious interaction, the effective screening
medium (ESM) method is exactly the method to do that.
Also, you didn't specify the keyword 'Atoms.UnitVectors.Unit' properly.
Third, please notice that if 'Band.dispersion on' is specified for geometry optimization, band
dispersion is calculated every optimization step, which is nothing but a useless calculation.
After getting the convergent structure, you can do calculations for analysis using *.dat#, while
of course you need to modify the input file for your purpose.
Regards,
TO
 |
| Re: Relaxation of MoS2 ( No.2 ) |
- Date: 2014/02/13 23:42
- Name: Artem <artem.pulkin@epfl.ch>
- Dear Taisuke,
I appreciate your prompt reply. I followed your suggestions and it worked like a charm.
Specifically, switching to LDA spin-unresolved calculation and steepest descent method produces a reasonable atomic structure. Of course, the band structure gets improved by increasing the basis as you mentioned rightly.
I would like to draw your attention now to spin-orbit relaxation. Monolayer MoS2 has a honeycomb lattice structure. The only degree of freedom allowed for this system (except the lattice constant) is an out-of-plane displacement of Sulphur atoms, let's call it "x". I fixed the rest of coordinates in my relaxation and plotted total energy vs x (blue dots):
http://s23.postimg.org/ki9l45ynv/weird_openmx_relaxation.png
As you can see it is a nice parabolic minimum. Then, I performed 5 steps of steepest descent relaxation (red dots). I started from configuration quite close to the minimum (red vertical line). The system immidiately moved away from equilibrium.
I would suggest that the forces computed in my system are wrong. Can you comment on this? Is this a methodological problem, compilation problem or, maybe, a bug?
Here is my input file:
System.CurrrentDirectory ./
System.Name mos2_1l
level.of.stdout 1
level.of.fileout 1
Species.Number 2
<Definition.of.Atomic.Species
Mo Mo7.0-s2p2d1 Mo_CA13
S S7.0-s1p1d1 S_CA13
Definition.of.Atomic.Species>
Atoms.UnitVectors.Unit Ang
<Atoms.UnitVectors
3.160 0.000 0.000
1.580 2.736640276 0.00
0.00000000 0.00000000 100.0
Atoms.UnitVectors>
Atoms.Number 3
Atoms.SpeciesAndCoordinates.Unit Frac
<Atoms.SpeciesAndCoordinates
1 Mo 0.3333333333 0.3333333333 0.0 5.0 9.0
2 S -0.3333333333 -0.3333333333 -0.01572 1.5 4.5
3 S -0.3333333333 -0.3333333333 0.01572 2.0 4.0
Atoms.SpeciesAndCoordinates>
<MD.Fixed.XYZ
1 1 1 1
2 1 1 0
3 1 1 0
MD.Fixed.XYZ>
scf.XcType LSDA-CA
scf.SpinPolarization nc
scf.ElectronicTemperature 300.0
scf.energycutoff 200.0
scf.maxIter 100
scf.EigenvalueSolver band
scf.Kgrid 7 7 1
scf.Mixing.Type rmm-diis
scf.Init.Mixing.Weight 0.30
scf.Min.Mixing.Weight 0.001
scf.Max.Mixing.Weight 0.400
scf.Mixing.History 7
scf.Mixing.StartPulay 5
scf.criterion 1.0e-10
scf.spinorbit.coupling on
MD.Type opt
MD.maxIter 5
MD.Opt.criterion 1.0e-5
|
| Re: Relaxation of MoS2 ( No.3 ) |
- Date: 2014/02/17 11:59
- Name: T. Ozaki
- Hi,
Thank you very much for drawing my attention to the problem.
I could also reproduce the unexpected behavior, and tried to figure out what's happening.
It turned out that the problem comes from the contribution of Tr(EDM*dS/dR) in the force
calculation, where EDM is the energy density matrix and dS/dR is the derivative of overlap
matrix with respect to atomic position R. Since EDM is not involved during the SCF calculation,
EDM is not calculated every SCF step, but calculated once every five SCF steps to reduce the
computational cost in the current version. But I found that actually this causes the problem.
I have changed the code so that the EDM is calculated every SCF step, and performed the
calculation by varying the height of S atoms.
The result I obtained within LDA is as follows:
1.530 -91.263954488476 -0.020515412314
1.550 -91.265178143976 -0.011950572339
1.560 -91.265547818289 -0.007841104511
1.576 -91.265823325624 -0.001488010360
1.578 -91.265831166295 -0.000748699589
1.579 -91.265830778564 -0.000351428747
1.580 -91.265829934668 0.000040666402
1.590 -91.265755651033 0.003881999553
1.600 -91.265537766767 0.007560709297
1.630 -91.264068815209 0.018042524189
where the first, second, and third columns are the height of S atoms (Ang.), the total
energy (Hartree), and the z-component of force on atom 2 (S atom, see also my input file shown later).
Note that the total energy and force can be obtained from the *.out file.
The energy minimum is almost consistent with the height at which the force changes its sign.
But if we take a close look, there is an inconsistency that the energy minimum
is at 1.578 Ang, while the sign change happens in between 1.579 and 1.580 Ang.
I think that the inconsistency is caused by the functional form of LDA parameterized by
Ceperley-Alder that the the derivatives of the function of rs in the LDA are discontinuous
at rs=1.
To check above the statement, I have performed the calculation by varying the height of S
atoms but with the GGA-PBE functional, and obtained the following result.
1.530 -91.401345746158 -0.029146560980
1.550 -91.403217805450 -0.020532722667
1.560 -91.403912407658 -0.016396032831
1.576 -91.404702821204 -0.010001439706
1.582 -91.404899516081 -0.007660269112
1.590 -91.405083861309 -0.004588777335
1.597 -91.405169753448 -0.001996435997
1.600 -91.405186316712 -0.000878800229
1.601 -91.405188647540 -0.000506212158
1.602 -91.405189528408 -0.000134124472
1.603 -91.405189115321 0.000233572341
1.604 -91.405187421906 0.000593520559
1.610 -91.405148025406 0.002756368553
1.630 -91.404669444655 0.009695506816
In this case, the energy minimum is consistent with the height at which the force changes its sign.
The energy minimum is at 1.602 Ang, and the sign change of force happens in between 1.602 and 1.603 Ang.
I will release a patch to fix the problem soon.
Best regards,
TO
P.S.
I used the following input file with different heights of S atoms for the calculations.
The GGA calculation was also performed by the input file with the specification of GGA-PBE.
-------------------------------------
System.CurrrentDirectory ./
System.Name m0
level.of.stdout 1
level.of.fileout 0
Species.Number 2
<Definition.of.Atomic.Species
Mo Mo7.0-s2p2d1 Mo_CA13
S S7.0-s1p1d1 S_CA13
Definition.of.Atomic.Species>
Atoms.UnitVectors.Unit Ang
<Atoms.UnitVectors
3.160 0.000 0.000
1.580 2.736640276 0.00
0.00000000 0.00000000 100.0
Atoms.UnitVectors>
Atoms.Number 3
Atoms.SpeciesAndCoordinates.Unit Frac
<Atoms.SpeciesAndCoordinates
1 Mo 0.3333333333 0.3333333333 0.0 5.0 9.0
2 S -0.3333333333 -0.3333333333 -0.01530 1.5 4.5
3 S -0.3333333333 -0.3333333333 0.01530 2.0 4.0
Atoms.SpeciesAndCoordinates>
#<MD.Fixed.XYZ
#1 1 1 1
#2 1 1 0
#3 1 1 0
#MD.Fixed.XYZ>
scf.XcType LSDA-CA # GGA-PBE
scf.SpinPolarization nc
scf.ElectronicTemperature 300.0
scf.energycutoff 200.0
scf.maxIter 100
scf.EigenvalueSolver band
scf.Kgrid 7 7 1
scf.Mixing.Type rmm-diis
scf.Init.Mixing.Weight 0.30
scf.Min.Mixing.Weight 0.001
scf.Max.Mixing.Weight 0.400
scf.Mixing.History 30
scf.Mixing.StartPulay 5
scf.criterion 1.0e-10
scf.spinorbit.coupling on
MD.Type nomd
MD.maxIter 5
MD.Opt.criterion 1.0e-5
|
| Re: Relaxation of MoS2 ( No.4 ) |
- Date: 2014/02/18 21:42
- Name: Artem <artem.pulkin@epfl.ch>
- Dear Taisuke,
I tested relaxation with spinors and it seems to work now. Again, thank you for such prompt investigation and fixing this problem.
Could you please give some more information on how the forces are calculated in openmx under L(S)DA?
|
| Re: Relaxation of MoS2 ( No.5 ) |
- Date: 2014/02/19 09:48
- Name: T. Ozaki
- Hi,
How the forces are calculated in OpenMX can be found at
http://www.openmx-square.org/tech_notes/tech1-1_2.pdf
Also, the implementation of the NC-DFT in OpenMX can be found at
http://www.openmx-square.org/tech_notes/tech2-1_0.pdf
The calculation of forces in the NC-DFT basically follows that for the collinear case.
Regards,
TO
|
| Re: Relaxation of MoS2 ( No.6 ) |
- Date: 2014/02/19 20:47
- Name: Artem <artem.pulkin@epfl.ch>
- Dear Taisuke,
Finally, I am trying to relax a larger cell of MoS2 (35 atoms). I have several nodes 48 cores each at my disposal. Is it enough to use mpi parallelization only for one node? Should I use openmp for two nodes (96 cores)?
For scf I have set the following set of parameters (my cell is elongated along x):
Species.Number 2
<Definition.of.Atomic.Species
Mo Mo7.0-s3p3d2f1 Mo_PBE13
S S7.0-s4p3d3f2 S_PBE13
Definition.of.Atomic.Species>
scf.XcType GGA-PBE # LDA|LSDA-CA|LSDA-PW|GGA-PBE
scf.SpinPolarization nc # On|Off|NC
scf.ElectronicTemperature 300.0 # default=300 (K)
scf.energycutoff 300.0 # default=150 (Ry)
scf.maxIter 100 # default=40
scf.EigenvalueSolver band # DC|GDC|Cluster|Band
scf.Kgrid 2 10 1 # means n1 x n2 x n3
scf.Mixing.Type rmm-diisk # Simple|Rmm-Diis|Gr-Pulay|Kerker|Rmm-Diisk
scf.Init.Mixing.Weight 0.30 # default=0.30
scf.Min.Mixing.Weight 0.001 # default=0.001
scf.Max.Mixing.Weight 0.400 # default=0.40
scf.Mixing.History 7 # default=5
scf.Mixing.StartPulay 5 # default=6
scf.criterion 1.0e-10 # default=1.0e-6 (Hartree)
scf.spinorbit.coupling on
And here is my convergence history:
http://s30.postimg.org/vkbt7bomp/Mo_S2_largecell.png
With these parameters, I am able to go up to 1e-5, not below. After 100 iterations a new cycle starts. Is it possible to reach smaller errors somehow?
Regards,
Artem
|
| Re: Relaxation of MoS2 ( No.7 ) |
- Date: 2014/02/20 10:21
- Name: T. Ozaki
- Hi,
It would be better to use a relatively large value for
scf.Mixing.History 30 # default=5
In addition, the Kerker factor should be provided explicitly by the keyword:
scf.Kerker.factor
The default value for your system is found in the beginning of the standard output.
Also, did you perform a series of calculations in a systematic way to determine
the basis functions for the small system? I wonder that the basis functions you used
are rich for your purpose.
Above the statements can be found in the manual. I would hope that you try to accumulate
experiences by yourself.
Regards,
TO
|
| Re: Relaxation of MoS2 ( No.8 ) |
- Date: 2014/03/20 20:02
- Name: Artem <artem.pulkin@epfl.ch>
- Dear Taisuke,
While I solved the problem with self-consistent part, the relaxation of above system (35 atoms) takes a large number of steps. I employ bfgs method, the same is used in Quantum Espresso as far as I know.
In QE relaxation is quite fast and the forces decrease monotonically almost throughout the whole calculation.
Instead, in openmx the forces do not equilibrate:
<Steepest_Descent> |Maximum force| (Hartree/Bohr) = 0.000789956871
<Steepest_Descent> |Maximum force| (Hartree/Bohr) = 0.000620713779
<Steepest_Descent> |Maximum force| (Hartree/Bohr) = 0.000498580111
<Steepest_Descent> |Maximum force| (Hartree/Bohr) = 0.000394654521
<BFGS> |Maximum force| (Hartree/Bohr) = 0.000307225316
<BFGS> |Maximum force| (Hartree/Bohr) = 0.000248808315
<BFGS> |Maximum force| (Hartree/Bohr) = 0.000160689987
<BFGS> |Maximum force| (Hartree/Bohr) = 0.000145239726
<BFGS> |Maximum force| (Hartree/Bohr) = 0.000067285798
<BFGS> |Maximum force| (Hartree/Bohr) = 0.000083457239
<BFGS> |Maximum force| (Hartree/Bohr) = 0.000063815596
<BFGS> |Maximum force| (Hartree/Bohr) = 0.000067341760
<BFGS> |Maximum force| (Hartree/Bohr) = 0.000068037060
<BFGS> |Maximum force| (Hartree/Bohr) = 0.000052148000
<BFGS> |Maximum force| (Hartree/Bohr) = 0.000045205149
<BFGS> |Maximum force| (Hartree/Bohr) = 0.000031498338
<BFGS> |Maximum force| (Hartree/Bohr) = 0.000034217340
<BFGS> |Maximum force| (Hartree/Bohr) = 0.000034644054
<BFGS> |Maximum force| (Hartree/Bohr) = 0.000050190577
<BFGS> |Maximum force| (Hartree/Bohr) = 0.000049616861
<BFGS> |Maximum force| (Hartree/Bohr) = 0.000058685111
<BFGS> |Maximum force| (Hartree/Bohr) = 0.000027548231
<BFGS> |Maximum force| (Hartree/Bohr) = 0.000028017686
<BFGS> |Maximum force| (Hartree/Bohr) = 0.000026587374
<BFGS> |Maximum force| (Hartree/Bohr) = 0.000031404459
<BFGS> |Maximum force| (Hartree/Bohr) = 0.000031772019
<BFGS> |Maximum force| (Hartree/Bohr) = 0.000031911253
<BFGS> |Maximum force| (Hartree/Bohr) = 0.000030771722
<BFGS> |Maximum force| (Hartree/Bohr) = 0.000026123410
<BFGS> |Maximum force| (Hartree/Bohr) = 0.000019479758
<BFGS> |Maximum force| (Hartree/Bohr) = 0.000018381638
<BFGS> |Maximum force| (Hartree/Bohr) = 0.000020236511
<BFGS> |Maximum force| (Hartree/Bohr) = 0.000046570179
<BFGS> |Maximum force| (Hartree/Bohr) = 0.000411344091
<BFGS> |Maximum force| (Hartree/Bohr) = 0.000030619932
<BFGS> |Maximum force| (Hartree/Bohr) = 0.000021979848
<BFGS> |Maximum force| (Hartree/Bohr) = 0.000061041281
<BFGS> |Maximum force| (Hartree/Bohr) = 0.000024875600
<BFGS> |Maximum force| (Hartree/Bohr) = 0.000233745835
<BFGS> |Maximum force| (Hartree/Bohr) = 0.000026183841
<BFGS> |Maximum force| (Hartree/Bohr) = 0.000030896178
<BFGS> |Maximum force| (Hartree/Bohr) = 0.000675315002
<BFGS> |Maximum force| (Hartree/Bohr) = 0.000030015271
<BFGS> |Maximum force| (Hartree/Bohr) = 0.000038961093
<BFGS> |Maximum force| (Hartree/Bohr) = 0.000165525269
<BFGS> |Maximum force| (Hartree/Bohr) = 0.000086025869
<BFGS> |Maximum force| (Hartree/Bohr) = 0.000044530620
<BFGS> |Maximum force| (Hartree/Bohr) = 0.001303094050
<BFGS> |Maximum force| (Hartree/Bohr) = 0.000057928949
<BFGS> |Maximum force| (Hartree/Bohr) = 0.000040376672
<BFGS> |Maximum force| (Hartree/Bohr) = 0.000090594981
<BFGS> |Maximum force| (Hartree/Bohr) = 0.000022279857
<BFGS> |Maximum force| (Hartree/Bohr) = 0.000027967403
<BFGS> |Maximum force| (Hartree/Bohr) = 0.000017787001
<BFGS> |Maximum force| (Hartree/Bohr) = 0.000036975854
<BFGS> |Maximum force| (Hartree/Bohr) = 0.000038816560
<BFGS> |Maximum force| (Hartree/Bohr) = 0.000034110639
<BFGS> |Maximum force| (Hartree/Bohr) = 0.000047314067
<BFGS> |Maximum force| (Hartree/Bohr) = 0.000138425165
<BFGS> |Maximum force| (Hartree/Bohr) = 0.000031307831
<BFGS> |Maximum force| (Hartree/Bohr) = 0.000093851422
<BFGS> |Maximum force| (Hartree/Bohr) = 0.000271206519
<BFGS> |Maximum force| (Hartree/Bohr) = 0.000062731051
<BFGS> |Maximum force| (Hartree/Bohr) = 0.000049099813
<BFGS> |Maximum force| (Hartree/Bohr) = 0.000047435743
<BFGS> |Maximum force| (Hartree/Bohr) = 0.000032246803
<BFGS> |Maximum force| (Hartree/Bohr) = 0.000037673951
<BFGS> |Maximum force| (Hartree/Bohr) = 0.000044579842
<BFGS> |Maximum force| (Hartree/Bohr) = 0.000320476361
<BFGS> |Maximum force| (Hartree/Bohr) = 0.000026583336
<BFGS> |Maximum force| (Hartree/Bohr) = 0.000047562199
<BFGS> |Maximum force| (Hartree/Bohr) = 0.000053725667
<BFGS> |Maximum force| (Hartree/Bohr) = 0.000024672225
<BFGS> |Maximum force| (Hartree/Bohr) = 0.000059031681
<BFGS> |Maximum force| (Hartree/Bohr) = 0.000084176687
<BFGS> |Maximum force| (Hartree/Bohr) = 0.001281711031
<BFGS> |Maximum force| (Hartree/Bohr) = 0.000043181085
<BFGS> |Maximum force| (Hartree/Bohr) = 0.000029728355
<BFGS> |Maximum force| (Hartree/Bohr) = 0.000039410794
<BFGS> |Maximum force| (Hartree/Bohr) = 0.000119490774
<BFGS> |Maximum force| (Hartree/Bohr) = 0.000149828723
<BFGS> |Maximum force| (Hartree/Bohr) = 0.000185303368
<BFGS> |Maximum force| (Hartree/Bohr) = 0.000260756355
Is it possible to converge this one?
|
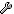| Re: Relaxation of MoS2 ( No.9 ) |
- Date: 2014/04/16 08:52
- Name: T. Ozaki
- Hi,
Instead of BFGS, could you try to employ RF or EF?
Also, I noticed that you have already achieved a sufficient convergence
that the maximum force is 0.000018381638 (Hartree/Borh).
I am wondering why you have to achieve a more precise convergence.
Did you check order of energy fluctuation?
Regards,
TO
|
|
This thread is locked.Only browsing is available.
Relaxation of MoS2