Manual of OpenFFT Version 1.1 (PDF)

Installation

Requirements:  OpenFFT requires FFTW3 (or FFTW3 wrappers such as those provided by the Intel MKL library), a C compiler, and an MPI library. Fortran users will also need a Fortran compiler to compile the Fortran sample programs. 

Step 1: Download and install FFTW3. Assume that FFTW3 is installed in /opt/fftw3. Those who already have the Intel MKL library or FFTW3 wrappers installed can skip this step. 

Step 2: Download and extract the OpenFFT tarball. Assume that OpenFFT is extracted to /opt/openfft1.1.

Step 3: Modify CC (the C compiler) and LIB (the library path to FFTW3) in makefile in the root folder of OpenFFT to reflect your environment. Fortran users also need to specify FC (the Fortran compiler) to compile the sample programs. Samples of CC (and FC) and LIB in several environments are given in makefile. 

CC = mpicc -O3 -I/opt/3/include -I./include
LIB = -L/opt/fftw3/lib -lfftw3
FC = mpif90 -O3 -I/opt/fftw3/include -I./include

Step 4: Issue the make command to compile and install the OpenFFT library. The library will be made available at /opt/openfft1.1/lib/libopenfft.a if successful. 

Step 5: Link the OpenFFT library to compile a user program. 

mpicc -O3 -o userprogram userprogram.c -I/opt/fftw3/include -I/opt/openfft1.1/include -L/opt/fftw3/lib -lfftw3 -L/opt/openfft1.1/lib -lopenfft
mpif90 -O3 -o userprogram userprogram.f90 -I/opt/fftw3/include -I/opt/openfft1.1/include -L/opt/fftw3/lib -lfftw3 -L/opt/openfft1.1/lib -lopenfft

Directory Structure

Directory structure of OpenFFT1.1 is as follows:
  • toplevel: this is where makefile is located, as well as README.
  • source: core source files of the package.
    • openfft_init_c2c_3d.c: initialization of complex-to-complex transforms. 
    • openfft_init_r2c_3d.c: initialization of real-to-complex transforms. 
    • openfft_exec_c2c_3d.c: execution of complex-to-complex transforms. 
    • openfft_exec_r2c_3d.c: execution of real-to-complex transforms. 
    • openfft_finalize.c: finalization of transforms.
    • openfft_dtime.c: built-in time measurement.
  • include: C and Fortran header files.
  • lib: the library file is installed here if successful. 
  • samples: sample programs for illustrating how to use OpenFFT.
    • C: C sample programs.
    • FORTRAN: Fortran sample program.s
  • doc: documents on the website of OpenFFT.

Sample Programs

Domain Decomposition

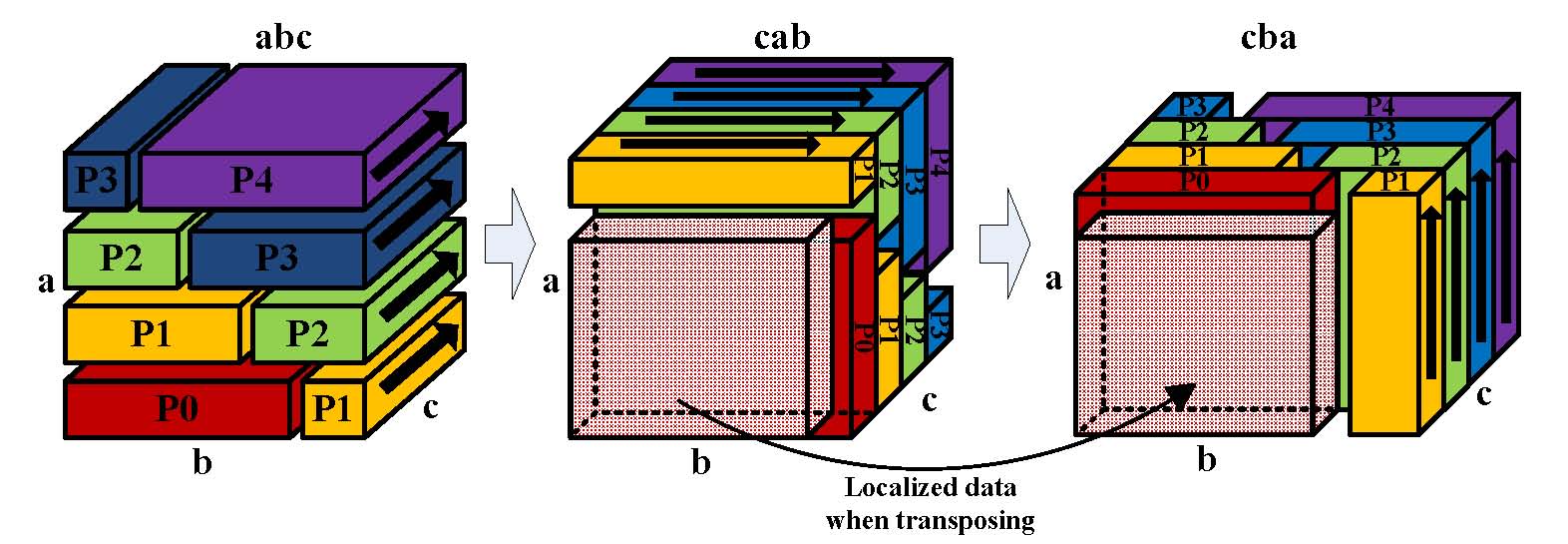
OpenFFT adopts a 2-D decomposition method that is capable of localizing data when transposing from one dimension to another to reduce the total volume of communication. Also, the decomposition is adaptive, and automatically switches between 1-D and 2-D depending on the number of processes and data size. OpenFFT decomposes in the order of abc, cab, and cba for performing the 1-D FFTs along the c-, b-, and a-axes, respectively. Please refer to the publications for detail.

Tuning of Communication

OpenFFT implements a number of communication patterns that can be selected manually by users or automatically by the auto-tuning feature when initializing with openfft_init_c2c_3d() or openfft_init_r2c_3d(). The communication patterns available are:
  • 0: auto-tuning of communication, where OpenFFT automatically performs tests with all of the following patterns and picks the best performer in run time (recommended for high performance).  
  • 1: MPI_Alltoallv.
  • 2: MPI_Isend and MPI_Irecv within sub-groups of 32 processes.
  • 3: MPI_Isend and MPI_Irecv with communication-computation overlap.
  • 4: MPI_Isend and MPI_Irecv within sub-groups of 32 processes with communication-computation overlap.
  • 5: MPI_Sendrecv.
  • 6: MPI_Isend and MPI_Irecv.
  • Others: default communication, which is 3.

Calling OpenFFT from a C User Program

Please refer to the C sample programs which illustrate how to call OpenFFT from a C user program. Basically, it involves several steps as follows. 

Step 1: Include the OpenFFT header file, openfft.h, in the program.

#include <openfft.h>

Step 2: Initialize OpenFFT by calling openfft_init_c2c_3d() for the c2c interface or openfft_init_r2c_3d() for the r2c interface.

openfft_init_c2c_3d(N1,N2,N3,
                     &My_Max_NumGrid,&My_NumGrid_In,My_Index_In,&My_NumGrid_Out,My_Index_Out,
                     offt_measure,measure_time,print_memory);

OR

openfft_init_r2c_3d(N1,N2,N3,
                     &My_Max_NumGrid,&My_NumGrid_In,My_Index_In,&My_NumGrid_Out,My_Index_Out,
                     offt_measure,measure_time,print_memory);

     Input:
    3 dimensions of data: N1, N2, N3.
    offt_measure for the tuning of communication (see Tuning of Communication, default 0).
    measure_time for the built-in time measurement function and print_memory for printing memory usage (0: disabled (default), 1: enabled).

     Output: arrays allocated and variables initialized.
             My_Max_NumGrid: the maximum number of grid points allocated to a process, used for allocating local arrays.
             My_NumGrid_In: the number of grid points allocated to a process upon starting.
             My_Index_In: the 6 indexes of grid points allocated to a process upon starting.
             My_NumGrid_Out: the number of grid points allocated to a process upon finishing.
             My_Index_Out: the 6 indexes of grid points allocated to a process upon finishing.

Step 3: After openfft_init_c2c_3d() or openfft_init_r2c_3d() is called, important variables are initialized, and can be used for allocating and initializing local input and output data arrays.

    • Allocate the local input and output data arrays based on My_Max_NumGrid, which is the maximum number of grid points allocated to a process during the transformation.  
input  = (dcomplex*)malloc(sizeof(dcomplex)*My_Max_NumGrid);
output = (dcomplex*)malloc(sizeof(dcomplex)*My_Max_NumGrid);

OR

input  = (double*)malloc(sizeof(double)*My_Max_NumGrid);
output = (dcomplex*)malloc(sizeof(dcomplex)*My_Max_NumGrid);
    • Initialize the local input array from the global input array. A process is allocated (My_NumGrid_In) grid points continuously from AasBbsCcs to AaeBbeCce of the 3-D global array, where:  
as = My_Index_In[0];
bs = My_Index_In[1];
cs = My_Index_In[2];
ae = My_Index_In[3];
be = My_Index_In[4];
ce = My_Index_In[5];

Step 4: Call openfft_exec_c2c_3d() or openfft_exec_r2c_3d() to transform input to output.

openfft_exec_c2c_3d(input, output); 

OR

openfft_exec_r2c_3d(input, output); 

Step 5:  Obtain the result stored in the local output array. Upon exiting, a process is allocated (My_NumGrid_Out) grid points continuously from CcsBbsAas to CceBbeAae of the 3-D global array, where:  

cs = My_Index_Out[0];
bs = My_Index_Out[1];
as = My_Index_Out[2];
ce = My_Index_Out[3];
be = My_Index_Out[4];
ae = My_Index_Out[5];

Step 6: Finalize the calculation by calling openfft_finalize(). 

openfft_finalize();

Calling OpenFFT from a Fortran User Program

Please refer to the Fortran sample programs which illustrate how to call OpenFFT from a Fortran user program. Basically, it is similar to calling from C, except for the indexes that must be incremented by 1.  

Step 1: Include the Fortran interface and the standard iso_c_binding module for defining the equivalents of C types (integer(C_INT) for int, real(C_DOUBLE) for double, complex(C_DOUBLE_COMPLEX) for dcomplex,  etc.).

use, intrinsic :: iso_c_binding
include 'openfft.fi'  

Step 2: Initialize OpenFFT by calling openfft_init_c2c_3d() for the c2c interface or openfft_init_r2c_3d() for the r2c interface.

 openfft_init_c2c_3d(%VAL(N1),%VAL(N2),%VAL(N3),&
       My_Max_NumGrid,My_NumGrid_In,My_Index_In,My_NumGrid_Out,My_Index_Out,&
       %VAL(offt_measure),%VAL(measure_time),%VAL(print_memory))

OR

openfft_init_r2c_3d(%VAL(N1),%VAL(N2),%VAL(N3),&
       My_Max_NumGrid,My_NumGrid_In,My_Index_In,My_NumGrid_Out,My_Index_Out,&
       %VAL(offt_measure),%VAL(measure_time),%VAL(print_memory))

     Input:
    3 dimensions of data: N1, N2, N3.
    offt_measure for the tuning of communication (see Tuning of Communication, default 0).
    measure_time for the built-in time measurement function and print_memory for printing memory usage (0: disabled (default), 1: enabled).

     Output: arrays allocated and variables initialized.
             My_Max_NumGrid: the maximum number of grid points allocated to a process, used for allocating local arrays.
             My_NumGrid_In: the number of grid points allocated to a process upon starting.
             My_Index_In: the 6 indexes of grid points allocated to a process upon starting.
             My_NumGrid_Out: the number of grid points allocated to a process upon finishing.
             My_Index_Out: the 6 indexes of grid points allocated to a process upon finishing.

Step 3: After openfft_init_c2c_3d() or openfft_init_r2c_3d() is called, important variables are initialized, and can be used for allocating and initializing local input and output data arrays.

    • Allocate the local input and output data arrays based on My_Max_NumGrid, which is the maximum number of grid points allocated to a process during the transformation.  
allocate(input(My_Max_NumGrid))
allocate(output(My_Max_NumGrid))
    • Initialize the local input array from the global input array. A process is allocated (My_NumGrid_In) grid points continuously from AasBbsCcs to AaeBbeCce of the 3-D global array, where:  
as = My_Index_In(1) + 1
bs = My_Index_In(2) + 1
cs = My_Index_In(3) + 1
ae = My_Index_In(4) + 1
be = My_Index_In(5) + 1
ce = My_Index_In(6) + 1

Step 4: Call openfft_exec_c2c_3d() or openfft_exec_r2c_3d() to transform input to output.

openfft_exec_c2c_3d(input, output); 

OR

openfft_exec_r2c_3d(input, output); 

Step 5:  Obtain the result stored in the local output array. Upon exiting, a process is allocated (My_NumGrid_Out) grid points continuously from CcsBbsAas to CceBbeAae of the 3-D global array, where:  

cs = My_Index_Out(1) + 1
bs = My_Index_Out(2) + 1
as = My_Index_Out(3) + 1
ce = My_Index_Out(4) + 1
be = My_Index_Out(5) + 1
ae = My_Index_Out(6) + 1

Step 6: Finalize the calculation by calling openfft_finalize(). 

openfft_finalize()

Complex-to-complex and Real-to-complex Transforms

While the sizes of the input and output arrays of the c2c transform stay unchanged, i.e., a complex input array of size N1xN2xN3 will have a corresponding complex output array of the same size N1xN2xN3, the size of the complex output array is only about half of that of the real input array of the r2c transform, i.e., a real input array of size N1xN2xN3 will have a corresponding complex output array of the size N1xN2x(N3/2+1). This means both computational cost and memory usage of an r2c transform are only about half those of a c2c one. Please refer to the C and Fortran examples for illustration of input and output data manipulation. 

Benchmarks

The figures below show some benchmark results with OpenFFT and a couple of other packages taken on several machines (complex-to-complex transforms with FFTW3 as the FFT engine, except for P3DFFT, where the r2c interface is used with 2x real numbers for equivalence of 1x complex numbers, and FFTE, which employs its own FFT engine). The latest official versions are utilized, as of November 2014. 

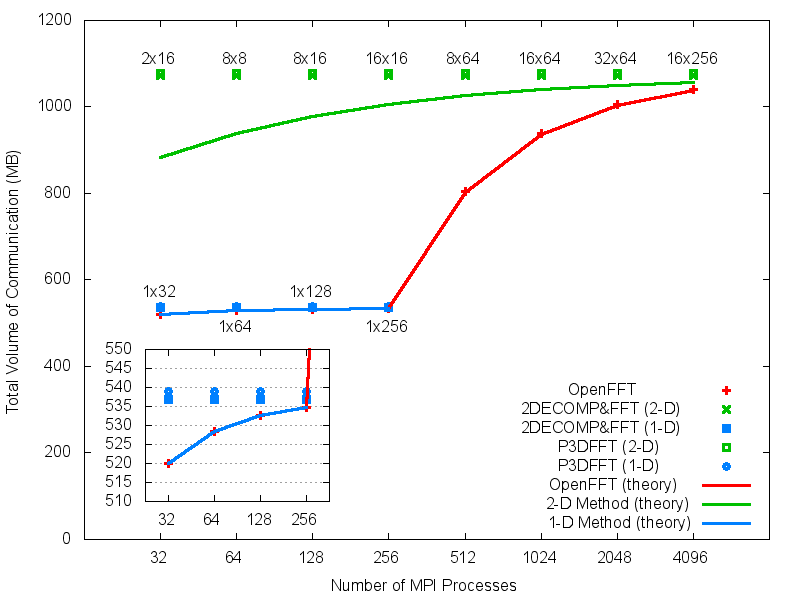
(a) Theoretical and practical volumes of communication (256^3). The practical volume is reported by the MPI profiler on the K computer.



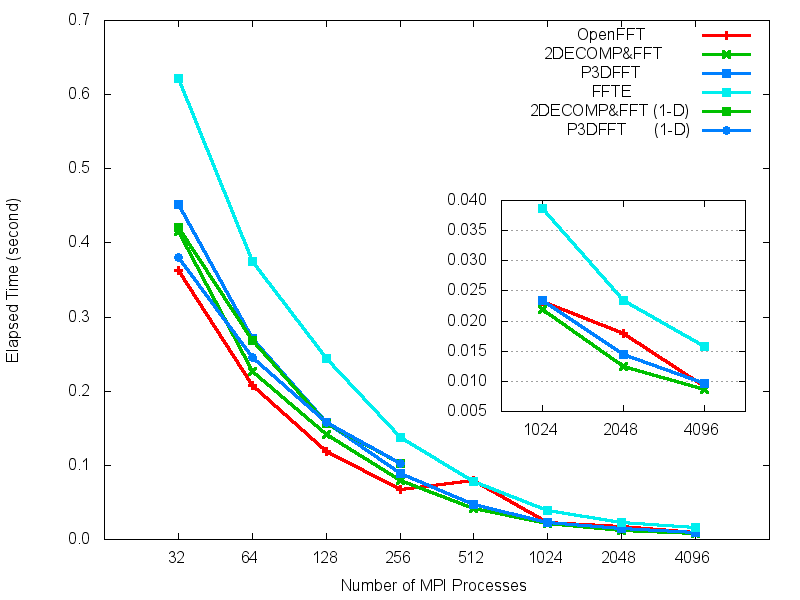
(b) Cray XC30 (512^3).



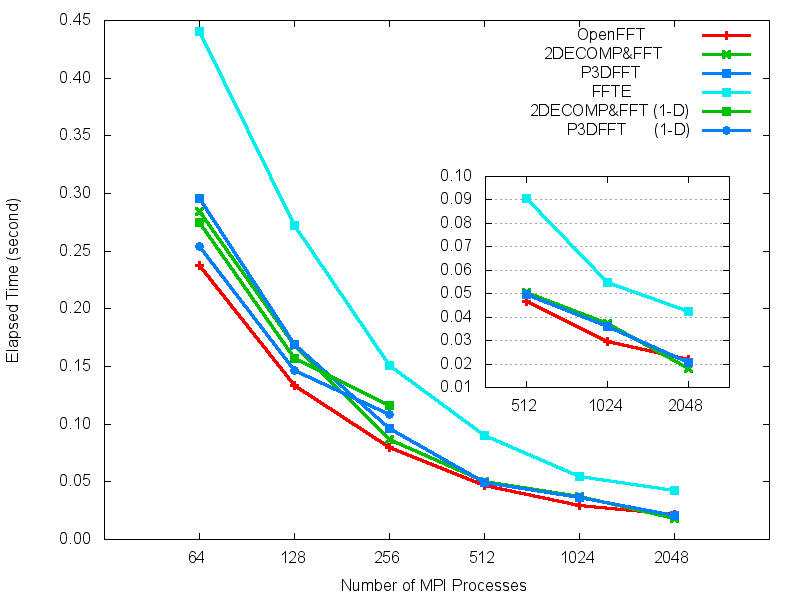
(c) SGI InfiniBand Machine (512^3).



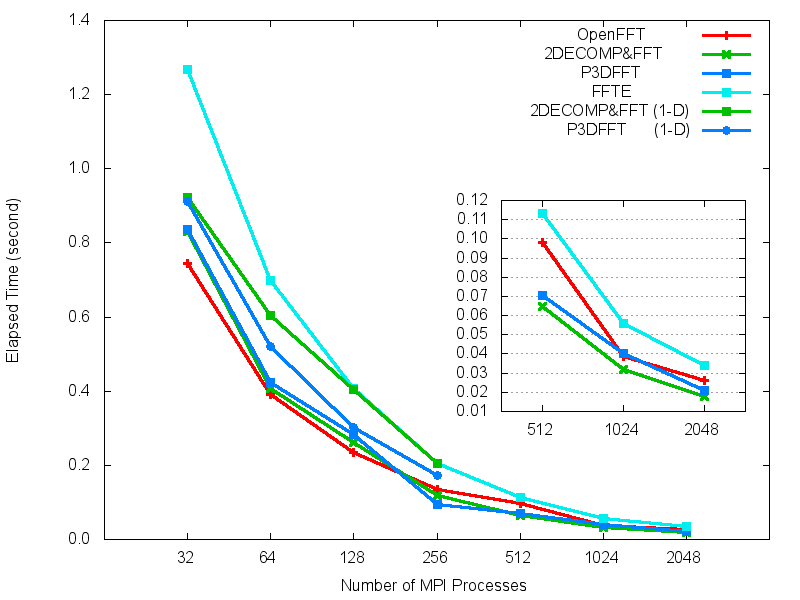
(d) Fujitsu FX10 (512^3).



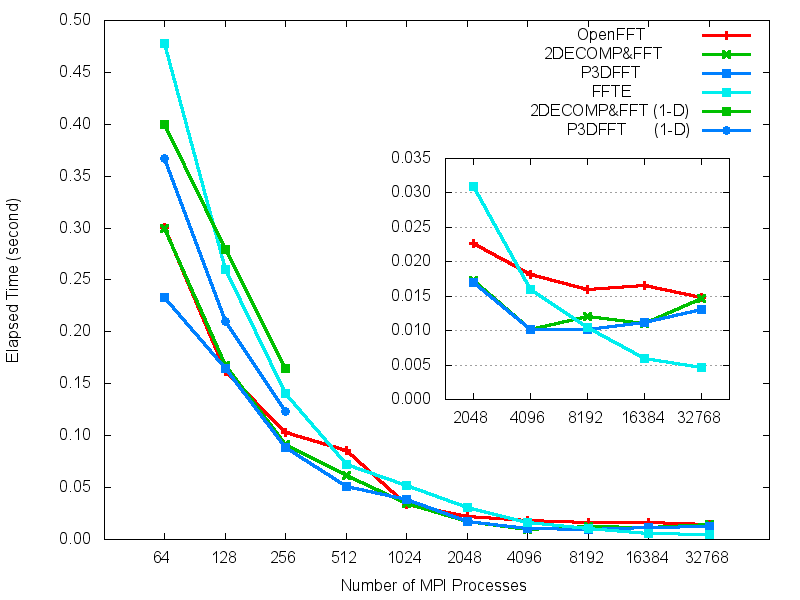
(e) K computer (512^3).