Next: Running again the step Up: Step 3: The transmission, Previous: Real-space charge/spin current density Contents Index
In the step 3, transmission eigenchannels are calculated optionally. Parameters for this calculation are as follows:
NEGF.tran.Channel on # default on
NEGF.Channel.Nkpoint 1 # default=1
<NEGF.Channel.kpoint
0.0 0.0
NEGF.Channel.kpoint>
# default 0.0 0.0
NEGF.Channel.Nenergy 1 # default=1
<NEGF.Channel.energy
0.0
NEGF.Channel.energy>
# default 0.0
NEGF.Channel.Num 5 # defualt=5(for collinear), 10(for Non-collinear)
NEGF.tran.Channel
If NEGF.tran.Channel is set to on,
the eigenchannel is calculated.
NEGF.Channel.Nkpoint, <NEGF.Channel.kpoint,
NEGF.Channel.kpoint>
These keywords specify the k point, at which eigenchannels are calculated.
Please write a ![]() points per one line
between
points per one line
between <NEGF.Channel.kpointand NEGF.Channel.kpoint>;
the total number of ![]() is
is NEGF.Channel.Nkpoint.
The coordinate of the ![]() is two dimensional fractional coordinate;
is two dimensional fractional coordinate;
![]() should be specified as coefficients of two reciprocal lattice vector
perpendicular to the transmittion direction.
should be specified as coefficients of two reciprocal lattice vector
perpendicular to the transmittion direction.
NEGF.Channel.Nenergy, <NEGF.Channel.energy,
NEGF.Channel.energy>
These keywords specify the energy, at which eigenchannels are calculated.
Please write a energy per one line between
<NEGF.Channel.energy and NEGF.Channel.energy>;
the total number of energies is NEGF.Channel.Nenergy.
The unit should be [eV] and the energy should be measured from the
electrochemical potential of the left lead.
NEGF.Channel.Num
It specifies the number of eigenchannels that are printed
in the real space representation.
In each ![]() , energy, spin,
, energy, spin,
NEGF.Channel.Num eigenchannels in descending order about
transmission eigenvalues are printed in the Gaussian cube format;
the real and imaginary part is printed separately.
In the calculation of eigenchannels, openmx makes the following standard output:
**************************************************
Calculation of transmission eigenchannels starts
**************************************************
File index : negf-8zgnr-0.3.traneval#k_#E_#spin negf-8zgnr-0.3.tranevec#k_#E_#spin
myid0 = 0, #k : 0, N_{ort} / N_{nonort} : 380 / 380
PE 0 generates ./negf-8zgnr-0.3.traneval0_0_0 . Sum(eigenval) : 0.031643
PE 0 generates ./negf-8zgnr-0.3.traneval0_0_1 . Sum(eigenval) : 0.000508
Eigenchannel calculation finished
They are written in plottable files.
File index : negf-8zgnr-0.3.tranec#k_#E_#spin_#branch_r.cube(.bin)
negf-8zgnr-0.3.tranec#k_#E_#spin_#branch_i.cube(.bin)
./negf-8zgnr-0.3.tranec0_0_0_0_r.cube ./negf-8zgnr-0.3.tranec0_0_0_0_i.cube
./negf-8zgnr-0.3.tranec0_0_0_1_r.cube ./negf-8zgnr-0.3.tranec0_0_0_1_i.cube
./negf-8zgnr-0.3.tranec0_0_0_2_r.cube ./negf-8zgnr-0.3.tranec0_0_0_2_i.cube
./negf-8zgnr-0.3.tranec0_0_0_3_r.cube ./negf-8zgnr-0.3.tranec0_0_0_3_i.cube
./negf-8zgnr-0.3.tranec0_0_0_4_r.cube ./negf-8zgnr-0.3.tranec0_0_0_4_i.cube
./negf-8zgnr-0.3.tranec0_0_1_0_r.cube ./negf-8zgnr-0.3.tranec0_0_1_0_i.cube
./negf-8zgnr-0.3.tranec0_0_1_1_r.cube ./negf-8zgnr-0.3.tranec0_0_1_1_i.cube
./negf-8zgnr-0.3.tranec0_0_1_2_r.cube ./negf-8zgnr-0.3.tranec0_0_1_2_i.cube
./negf-8zgnr-0.3.tranec0_0_1_3_r.cube ./negf-8zgnr-0.3.tranec0_0_1_3_i.cube
./negf-8zgnr-0.3.tranec0_0_1_4_r.cube ./negf-8zgnr-0.3.tranec0_0_1_4_i.cube
In this case, 22 files,
negf-8zgnr-0.3.treval0_0_0, negf-8zgnr-0.3.tranevec0_0_0,
negf-8zgnr-0.3.tranec0_0_0_0_r.cube - negf-8zgnr-0.3.tranec0_0_1_4_r.cube,
negf-8zgnr-0.3.tranec0_0_0_0_i.cube - negf-8zgnr-0.3.tranec0_0_1_4_i.cube,
are generated.
.traneval{#k}_{#E}_{#s}
This file contains transmission eigenvalues of all eigenchannels in
the {#k}th k, {#E}th energy, and {#s}th spin.
.tranevec{#k}_{#E}_{#s}
This file contains LCAO components of all eigenchannels in
the {#k}th k, {#E}th energy, and {#s}th spin.
e. g. / negf-chain.tranevec0_0_0
***********************************************************
***********************************************************
Eigenvalues and LCAO coefficients
at the k-points specified in the input file.
***********************************************************
***********************************************************
# of k-point = 0
k2= 0.00000 k3= 0.00000
# of Energy = 0
e= 0.00000
Spin = Up
Real (Re) and imaginary (Im) parts of LCAO coefficients
1 2 3 4
0.9778 0.0000 0.0000 0.0000
Re Im Re Im Re Im Re Im
1 C 0 s -0.00000 -0.00000 -0.00000 0.00000 0.00000 0.00000 -0.00000 0.00000
1 s -0.00000 -0.00000 -0.00000 -0.00000 0.00000 -0.00000 0.00000 -0.00000
0 px -0.63002 -1.49377 -0.14466 0.00019 0.01644 -0.00032 -0.07885 0.00095
0 py 0.00000 0.00000 0.00000 0.00000 -0.00000 0.00000 0.00000 0.00000
0 pz 0.00000 -0.00000 0.00000 -0.00000 -0.00000 -0.00000 -0.00000 -0.00000
2 C 0 s -0.00000 -0.00000 -0.00000 -0.00000 0.00000 -0.00000 0.00000 -0.00000
1 s 0.00000 0.00000 -0.00000 -0.00000 -0.00000 0.00000 -0.00000 0.00000
0 px 0.18040 -0.03816 -0.00452 0.00009 -0.00545 -0.00010 -0.01970 -0.00004
0 py -0.00000 -0.00000 -0.00000 0.00000 0.00000 0.00000 0.00000 0.00000
0 pz 0.00000 -0.00000 -0.00000 0.00000 -0.00000 -0.00000 -0.00000 -0.00000
3 C 0 s 0.00000 0.00000 0.00000 -0.00000 -0.00000 0.00000 -0.00000 0.00000
1 s -0.00000 -0.00000 0.00000 0.00000 0.00000 -0.00000 0.00000 -0.00000
0 px 2.06634 0.40490 0.11067 0.00023 -0.06068 0.00009 -0.06690 -0.00042
0 py 0.00000 0.00000 0.00000 -0.00000 -0.00000 0.00000 -0.00000 0.00000
0 pz 0.00000 0.00000 0.00000 0.00000 -0.00000 -0.00000 0.00000 -0.00000
4 C 0 s 0.00000 0.00000 0.00000 0.00000 -0.00000 -0.00000 -0.00000 -0.00000
1 s -0.00000 -0.00000 -0.00000 -0.00000 -0.00000 0.00000 -0.00000 0.00000
.tranec{#k}_{#E}_{#s}_{#c}_r.cube,
.tranec{#k}_{#E}_{#s}_{#c}_i.cube
This file contains the real or the imaginary part of the eigenchannel in the Gaussian cube format. We can display isosurfaces from this files by using VESTA, XCrysDen, etc.
For example, eigenchannels in 8-zigzag graphene nanoribbon with an antiferromagnetic junction under a finite bias voltage of 0.3 V is shown in Fig. 35.
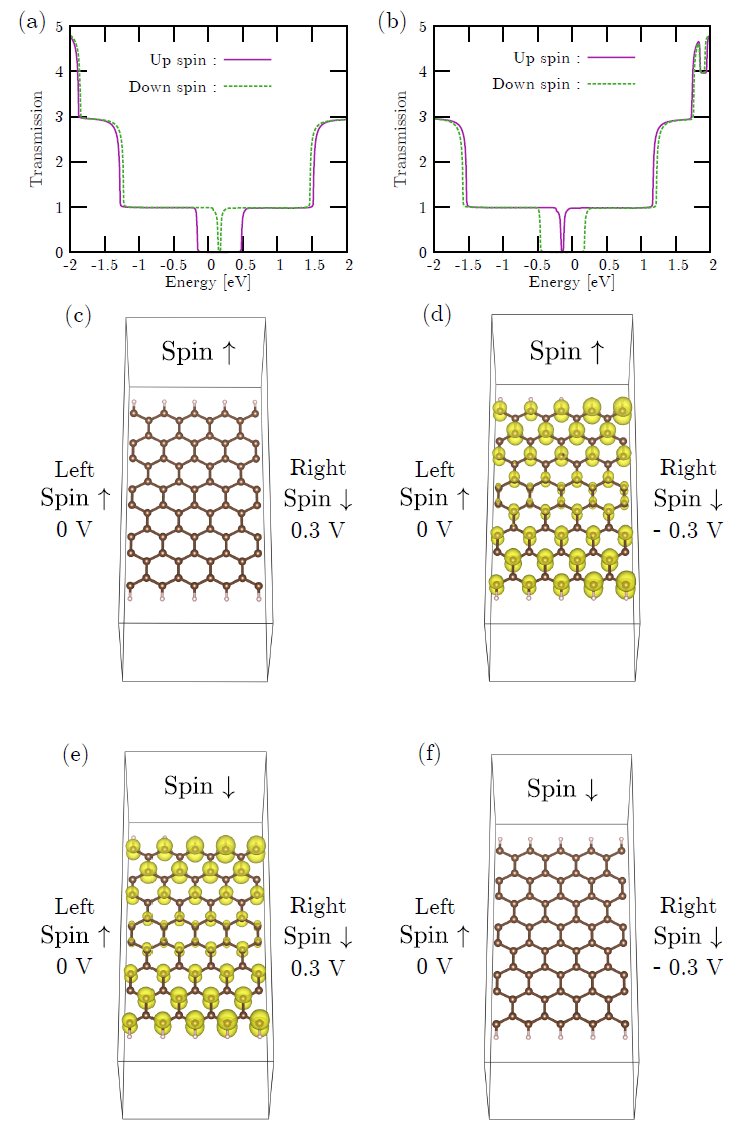 |
2016-04-03