Using cube files of either System.Name.v0.cube or System.Name.v1.cube,
one can calculate work functions of metals. The work function is defined by
where ![$E[N]$](img386.png) and
and ![$E[N-1]$](img387.png) are the total energies of the
are the total energies of the 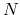 -electron and
-electron and 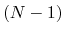 -electron systems,
respectively, and
-electron systems,
respectively, and 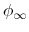 and
and 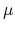 are the potential at the infinite distance from the surface
and the chemical potential, respectively. The second line of Eq. (11) can be obtained
by the Janak theorem [89] as
are the potential at the infinite distance from the surface
and the chemical potential, respectively. The second line of Eq. (11) can be obtained
by the Janak theorem [89] as
![$E[N-1]-E[N]=\int dn \partial E/\partial n = -\mu$](img391.png) ,
where
,
where 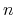 is an occupation number of an one-particle eigenstate on the Fermi surface,
is an occupation number of an one-particle eigenstate on the Fermi surface, 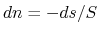 defined with the area of the Fermi surface
defined with the area of the Fermi surface 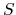 and an infinitesimal area
and an infinitesimal area 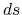 , and the surface
integral is performed over the Fermi surface.
Since the work function is a quantity associated to a surface, we need to introduce a slab model
as shown in Fig. 54(a). As an example, we consider an aluminum slab, where
the layer thickness is 5 and the vacuum of about 60 Å is taken into account along the
, and the surface
integral is performed over the Fermi surface.
Since the work function is a quantity associated to a surface, we need to introduce a slab model
as shown in Fig. 54(a). As an example, we consider an aluminum slab, where
the layer thickness is 5 and the vacuum of about 60 Å is taken into account along the 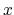 -axis
together with the effective screening medium (ESM) method in Sec. 47, where
'ESM.switch=on1' is used, to avoid the interaction between the periodic slabs.
The SCF calculation can be performed using an input file 'Al111_WorkFunc_0E.dat' as follows:
-axis
together with the effective screening medium (ESM) method in Sec. 47, where
'ESM.switch=on1' is used, to avoid the interaction between the periodic slabs.
The SCF calculation can be performed using an input file 'Al111_WorkFunc_0E.dat' as follows:
% mpirun -np 28 ./openmx Al111_WorkFunc_0E.dat
After the calculation is completed normally, you obtain a cube file of 'Al111_WorkFunc_0E.v0.cube'.
To analyze the cube file, you can utilize a post-processing code of 'gcube2oned.c' in the directory 'source',
which can be compiled as
% gcc gcube2oned.c -lm -o gcube2oned
After copying the executable code 'gcube2oned' to your working directory, you can transform
the data of 3D cube data to an 1D data along a chosen direction,
in this case '1' corresponding to the a-axis, by integrating over the remaining 2D (bc-plane)
as follows:
% gcube2oned Al111_WorkFunc_0E.v0.cube 1 > 1d_pot.txt
Figure 54:
(a) A slab model consisting of Al atoms, where the layer thickness is 5 and the vacuum
of 60 Å is taken into account along the 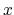 -axis.
(b) A slab model consisting of Al atoms, where the layer thickness is 5 and the vacuum
of 60 Å is taken into account along the
-axis.
(b) A slab model consisting of Al atoms, where the layer thickness is 5 and the vacuum
of 60 Å is taken into account along the 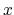 -axis. In addtion to the Al layers,
the 6 layers consisting of empty atoms are introduced for both the surfaces so that
the tail of wave function towards the vacuum region can be accurately described.
-axis. In addtion to the Al layers,
the 6 layers consisting of empty atoms are introduced for both the surfaces so that
the tail of wave function towards the vacuum region can be accurately described.
|
|
In the obtained file '1d_pot.txt', the first, second, and third columns correspond to
the serian number of grid, the position (Å) along the a-axis, and a 1D potential (Hartree)
averaged over the bc-plane. In case of the 1D potential along the b or c-axis,
you can specify '2' or '3' as an argument of 'gcube2oned'. In Fig. 55 we show
the 1D potentials for the Al(111) surface along the a-axis which is perpendicular to the surface.
The number of layers consisting of empty atoms is systematically changed from 0 to 7 for both the surfaces.
As shown in Fig. 54, the layers consisting of empty atoms are taken into account
so that the tail of wave function towards the vacuum region can be accurately described.
The input files used for the calculations are
'Al111_WorkFunc_%E.dat', where % varies from 0 to 7, which are all available
in the directory 'work'.
The potential 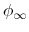 in Eq. (11) can be obtained from that at around 70 Å,
while the chemical potential
in Eq. (11) can be obtained from that at around 70 Å,
while the chemical potential 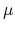 can be found from the out file. Since the potential at around
70 Å is almost zero, the work function is basically determined by the chemical potential in the cases.
Then, the calculated values using Eq. (11) are plotted as a function of the number of
empty layers in Fig. 56.
One can see that the work function of the Al(111) surface reaches to the convergence
at the 2 empty layers, implying adding the 2 empty layers is sufficient to obtain the convergent result.
can be found from the out file. Since the potential at around
70 Å is almost zero, the work function is basically determined by the chemical potential in the cases.
Then, the calculated values using Eq. (11) are plotted as a function of the number of
empty layers in Fig. 56.
One can see that the work function of the Al(111) surface reaches to the convergence
at the 2 empty layers, implying adding the 2 empty layers is sufficient to obtain the convergent result.
Figure 55:
1D potentials (Hartree) along the a-axis averaged over the bc-plane,
which are obtained from the v0.cube files. The number of layers consisting of empty atoms
is systematically changed from 0 to 7. The input files used for the calculations are
'Al111_WorkFunc_%E.dat', where % varies from 0 to 7, which are all available
in the directory 'work'.
|
|
Figure 56:
Work function (eV) of the Al(111) surface as a function of the number of empty layers.
The values can be obtained based on Eq. (11) and the calculations shown
in Fig. 55.
|
|
In Table 11 we show the calculated results of work function for five metals and
the corresponding experimental values. In all the calculations the 7 empty layers were introduced.
It is found that the calculated values are well compared to the experimental values.
The input files used for the calculations are 'Al111_WorkFunc_7E.dat', 'Cu111_WorkFunc_7E.dat',
'Ag111_WorkFunc_7E.dat', 'Au111_WorkFunc_7E.dat', and 'Pd111_WorkFunc_7E.dat', which are all
available in the directory 'work'.
As for gapped systems Eq. (11) may not be valid in a rigorous sense.
However, you may be able to use Eq. (11) as an approximate treatment.
Especially for gapped systems with polar surfaces, you need to use the ESM method
in Sec. 47 to avoid the interaction between the periodic slabs.
Table 11:
Calculated work functions (eV) for five metals and the corresponding experimental values.
We note that the reported experimental values seem to vary in literatures, and we show one
of them in the table.
| |
OpenMX |
Expt. |
| Al(111) |
4.19 |
4.26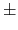 0.03 [129] 0.03 [129] |
| Cu(111) |
4.74 |
4.94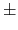 0.03 [130] 0.03 [130] |
| Ag(111) |
4.51 |
4.46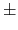 0.02 [131] 0.02 [131] |
| Au(111) |
5.33 |
5.26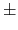 0.04 [132] 0.04 [132] |
| Pd(111) |
5.40 |
5.55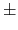 0.01 [133] 0.01 [133] |
![\includegraphics[width=12.0cm]{WorkFunc-Fig1.eps}](img394.png)
![\includegraphics[width=15.9cm]{WorkFunc-Fig2.eps}](img395.png)
![\includegraphics[width=13.0cm]{WorkFunc-Fig3.eps}](img396.png)