Ionization potential and electron affinity of gaseous systems
The ionization potential and electron affinity of gaseous systems can be calculated by a delta SCF method
with an exact Coulomb cutoff method [91].
With the exact Coulomb cutoff method, a calculation for a charged isolated system is possible even in the periodic
boundary condition.
What you need is to perform two calculations for the ground and ionized states of an isolated system, and
to calculate the difference of the total energies between them.
Let us illustrate calculations for ionization potential of gaseous systems.
The first example is a water molecule. One can perform a calculation for the ground state as
% mpirun -np 3 ./openmx H2O+0.dat | tee h2o+0.std
The input file 'H2O+0.dat' is available in the directory 'work'.
The geometry structure was optimized with the same computational condition before the calculation.
To avoid the Coulomb interaction between the supercells the exact Coulomb cutoff method [91]
is employed by the following keyword:
scf.coulomb.cutoff on # default=off, on|off
Even if the method is employed, where the cutoff radius for the Coulomb interaction is set
to the half of the lenght of the shortest lattice vector,
the cell size has to be large enough so that the Coulomb interaction
in the central cell can be properly calculated.
The calculation for the ionized state can be performed as
% mpirun -np 3 ./openmx H2O+1.dat | tee h2o+1.std
The input file 'H2O+1.dat' is available in the directory 'work'.
Compared to 'H2O+0.dat' the following keywords need to be changed:
scf.system.charge 1.0 # default=0.0
scf.coulomb.cutoff on # on|off, default=off
scf.SpinPolarization on # On|Off|NC
The system is positively charged up by the keyword 'scf.system.charge'.
The Coulomb divergence in the charged systems can be eliminated by using the exact Coulomb
cutoff method with 'scf.coulomb.cutoff'. The system may be spin-polarized after the ionization.
Thus, 'scf.SpinPolarization' is switched on.
After finishing the two caculations you may obtain the total energies from the out files as
Ground state: -17.477268421216 (Hartree)
Charged state of +1: -17.010776518028 (Hartree)
Then, the ionization potential  ,
defined to be (total energy of charged state of +1) - (total energy of the ground state),
is calculated as
,
defined to be (total energy of charged state of +1) - (total energy of the ground state),
is calculated as
The obtained value of 12.69 eV is well compared to an experimental value of 12.65 eV [96].
As well as the ionization potential, one can calculate the electron affinity,
defined to be (total energy of the ground state) - (total energy of charged state of -1),
of gaseous systems by specifying
scf.system.charge -1.0 # default=0.0
With 'scf.system.charge=-1.0', the system is negatively charged up by one additional electron.
The results for benchmark calculations of the ionization potential and electron affinity of gaseous systems
are shown in Table 13. We see that the calculated results of ionization potential are well
compared to experimental data, while the calculated electron affinities of some systems seem to deviate
from the experimental values especially for O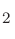 and Cl
and Cl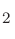 .
.
Table 13:
Calculated ionization potential and electron affinity of gaseous systems.
All the geometrical structures were optimized with the same computational condition before the calculations.
All the input files, which are listed below, used the calculations are available in the directory 'work'.
|
| Ionization potential |
|
|
|
| System |
Expt. (eV) |
Calc. (eV) |
Input files |
H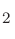 O O |
12.65 [96] |
12.69 |
H2O+0.dat, H2O+1.dat |
C H H |
11.43 [97] |
11.47 |
C2H2+0.dat, C2H2+1.dat |
C H H |
10.55 [97] |
10.57 |
C2H4+0.dat, C2H4+1.dat |
O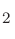 |
12.04 [97] |
12.85 |
O2+0.dat, O2+1.dat |
| CO |
14.01 [97] |
13.85 |
CO+0.dat, CO+1.dat |
| |
|
|
|
| Electron affinity |
|
|
|
| System |
Expt. (eV) |
Calc. (eV) |
Input files |
| OH |
1.81 [97] |
1.82 |
OH-0.dat, OH-1.dat |
O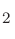 |
0.41 [97] |
-0.29 |
O2-0.dat, O2-1.dat |
Cl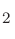 |
2.37 [97] |
0.96 |
Cl2-0.dat, Cl2-1.dat |
| CN |
3.88 [97] |
3.51 |
CN-0.dat, CN-1.dat |
| SiH |
1.27 [97] |
1.17 |
SiH-0.dat, SiH-1.dat |
|
![]() and Cl
and Cl![]() .
.