next up previous contents index
Next: Automatic determination of Kerker's Up: SCF convergence Previous: SCF convergence   Contents   Index

General

Seven charge mixing schemes in OpenMX Ver. 3.9 are available by the keyword 'scf.Mixing.Type':

In the first three schemes density matrices, which are regarded as a quantity in real space, are mixed to generate the input density matrix which can be easily converted into (spin) charge density. On the other hand, the charge mixing is made in Fourier space in the next three schemes: 'Kerker', 'RMM-DIISK', and 'RMM-DIISV'. The last scheme, 'RMM-DIISH', mixes Kohn-Sham Hamiltonian matrices, which may be suitable for the plus U method and the constraint schemes. Generally, it is easier to achieve SCF convergence in large gap systems using any mixing scheme. However, it would be difficult to achieve a sufficient SCF convergence in smaller gap and metallic systems, since a charge sloshing problem in the SCF calculations becomes serious often. To handle such difficult systems, three mixing schemes are currently available: 'Kerker', 'RMM-DIISK', and 'RMM-DIISV' methods. The three mixing schemes could be an effective way for achieving the SCF convergence of metallic systems. When 'Kerker', 'RMM-DIISK', or 'RMM-DIISV' is used, the following prescriptions are helpful to obtain the convergence of SCF calculations:

Figure 7: Convergence of the norm of residual density matrix or charge density in the SCF calculations using five mixing schemes of (a) a sialic acid molecule, (b) a Pt$_{13}$ cluster, and (c) a Pt$_{63}$ cluster. The input files are 'SialicAcid.dat', 'Pt13.dat', and 'Pt63.dat' in the directory 'work'.
\includegraphics[width=10.0cm]{SCF.eps}

In addition, the charge sloshing, which comes from charge components with long wave length, can be significantly suppressed by tuning Kerker's factor $\alpha $ by the keyword 'scf.Kerker.factor', where Kerker's metric is defined by

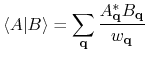$\displaystyle \langle A \vert B \rangle = \sum_{\bf q} \frac{A_{\bf q}^* B_{\bf q}}{w_{\bf q}}$      
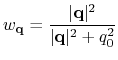$\displaystyle w_{\bf q} = \frac{ \vert{\bf q}\vert^2} {\vert {\bf q}\vert^2+ q_0^2}$      

$\displaystyle q_0 = \alpha \vert {\bf q}_{\rm min} \vert$      

where ${\bf q}_{\rm min}$ is the ${\bf q}$ vector with the minimum magnitude except 0-vector. A larger $\alpha $ significantly suppresses the charge sloshing, but leads to slower convergence. Since an optimum value depends on system, you may tune an appropriate value for your system.

Furthermore, the behavior of 'RMM-DIISK' can be controlled by the following keyword: 

   scf.Mixing.EveryPulay    5   # default = 1

The residual vectors in the Pulay-type mixing schemes tend to become linearly dependent on each other as the mixing steps accumulate, and the linear dependence among the residual vectors makes the convergence difficult. A way of avoiding the linear dependence is to do the Pulay-type mixing occasionally during the Kerker mixing. With this prescription, you can specify the frequency using the keyword 'scf.Mixing.EveryPulay'. For example, in case of 'scf.Mixing.EveryPulay=5', the Pulay-mixing is made at every five SCF iterations, while the Kerker-type mixing is used at the other steps. 'scf.Mixing.EveryPulay=1' corresponds to the conventional Pulay-type mixing. It is noted that the keyword 'scf.Mixing.EveryPulay' is supported for only 'RMM-DIISK', and the default value is '1'.

The above prescription works in some cases. But the most recommended prescription to accelerate the convergence is the following:

Since the Pulay-type mixing such as 'RMM-DIIS', 'RMM-DIISK', and 'RMM-DIISV' is based on a quasi Newton method, the convergence speed is governed by how a good approximate Hessian matrix can be found. As 'scf.Mixing.History' increases, the calculated Hessian may become more accurate.

In Fig. 7 a comparison of seven mixing schemes is shown for the SCF convergence for (a) a sialic acid molecule, (b) a Pt$_{13}$ cluster, and (c) a Pt$_{63}$ cluster, where the norm of residual density matrix or charge density can be found as NormRD in the file 'System.Name.out' and the input files are 'SialicAcid.dat', 'Pt13.dat', and 'Pt63.dat' in the directory 'work'. We see that 'RMM-DIISK' and 'RMM-DIISV' work with robustness for all the systems shown in Fig. 7. In most cases, 'RMM-DIISK' and 'RMM-DIISV' will be the best choice, while the use of 'Kerker' is required with a large 'scf.Kerker.factor' and a small 'scf.Max.Mixing.Weight' for quite difficult cases in which the convergence is hardly obtained. Also our experiences imply that 'RMM-DIISH' is suitable for the plus U method and the constraint schemes, while such a case is not shown in Fig. 7.

next up previous contents index
Next: Automatic determination of Kerker's Up: SCF convergence Previous: SCF convergence   Contents   Index