Closest Wannier functions to a given set of localized orbitals
The original has been published in Phys. Rev. B 110, 125115 (2024). See also a related website.

Abstract

A non-iterative method is presented to calculate the closest Wannier functions (CWFs) to a given set of localized guiding functions, such as atomic orbitals, hybrid atomic orbitals, and molecular orbitals, based on minimization of a distance measure function. It is shown that the minimization is directly achieved by a polar decomposition of a projection matrix via singular value decomposition, making iterative calculations and complications arising from the choice of the gauge irrelevant. The disentanglement of bands is inherently addressed by introducing a smoothly varying window function and a greater number of Bloch functions, even for isolated bands. In addition to atomic and hybrid atomic orbitals, we introduce embedded molecular orbitals in molecules and bulks as the guiding functions, and demonstrate that the Wannier interpolated bands accurately reproduce the targeted conventional bands of a wide variety of systems including Si, Cu, the TTF-TCNQ molecular crystal, and a topological insulator of Bi${}_2$Se${}_3$. We further show the usefulness of the proposed method for calculating effective atomic charges. These numerical results not only establish our proposed method as an efficient alternative for calculating WFs, but also suggest that the concept of CWF can serve as a foundation for developing novel methods to analyze electronic structures and calculate physical properties.

I INTRODUCTION

Wannier functions (WFs) [1, 2, 3] play a central role in analyzing electronic structures of real materials and advancing electronic structure methods along with density functional theory (DFT) [4] and the other electronic structure theories [5, 6]. A widely adopted method for calculating WFs involves maximizing their localization, which can be reformulated as minimizing the spread function characterizing the variance of the WFs in real space [7, 8]. The concept of maximal localization leads to an elegant formulation, resulting in maximally localized Wannier functions (MLWFs), and the following compact representation of the Hamiltonian allows us to analyze the electronic structures of real materials using a localized orbital picture. However, it is also recognized that the minimization of the spread function often encounters local minima, particularly in large-scale systems with complicated electronic structures [3]. To overcome this challenge, methods aimed at automated high-throughput Wannierisation have been developed [9, 10, 11]. In addition, other methods for generating (nonorthogonal) WFs have been proposed based on projection methods [12, 13, 14], which produce compact atomic like orbitals. The orthogonalization of such nonorthogonal orbitals obtained by the projection can be achieved using the Löwdin orthogonalization procedure [15, 16]. These orthogonalized orbitals are utilized as an initial guess of the WFs in the minimization of the spread function to obtain MLWFs [7, 17]. Apart from the role of the initial guess, it is worth noting that the Löwdin orthogonalized orbitals possess an important variational property, which in particular minimizes the sum of the squared distances between the orthogonal and original nonorthogonal orbitals in the Hilbert space [18]. As long as the original nonorthogonal orbitals are localized, the localization of the Löwdin orthogonalized orbitals in real space is guaranteed in a sense of minimization of the distance. In quantum chemistry, this property is leveraged to develop methods for generating localized orthogonal orbitals. These methods, which include the natural atomic and bond orbital method [19] and the intrinsic atomic orbital method (IAO) [20], involve obtaining orthogonalized orbitals through Löwdin type orthogonalization, giving heavy weight to occupied states via the density matrix. On the other hand, in solid state physics, the variational property inherent in the Löwdin orthogonalization has not yet been fully explored. This is because the Löwdin orthogonalization requires the calculation of $S^{-1/2}$ for the overlap matrix $S$, which causes numerical instability for nearly ill-conditioned matrices. Owing to this difficulty, advancements in methodologies along these lines appear to be slow. It should be mentioned that avoiding the calculation of $S^{-1/2}$ has already been proposed based on singular value decomposition (SVD) to calculate an initial guess of WFs for the maximal localization [8]. However, the relationship between the WFs obtained through this procedure and the variational principle has not been sufficiently discussed so far.

Our study aims to develop an efficient and robust method for generating the closest Wannier functions (CWFs) to a given set of localized guiding functions, based on a variational principle and polar decomposition of the projection matrix. We will demonstrate that exploiting the variational property leads to a versatile method that eliminates the need for iterative optimization and avoids complications related to the gauge choice. The projection method based on the polar decomposition has already been employed as a workaround [21, 22] with successful applications [23, 24]. However, to the best of our knowledge, no study has thoroughly discussed the mathematical and physical significance of this method based on the closest principle. Our study establishes the theoretical foundation by formulating the closest principle as a variational problem, and clarifies the relationship between the Löwdin orthogonalization and the polar decomposition. We will also introduce a smoothly varying window function that enables us to flexibly control targeted states to be Wannierized in a similar way to that proposed in Ref. [10]. The present study offers a more rigorous justification for these practices. With the theoretical advancement, the concept of CWF can serve as a foundation for developing novel methods to analyze electronic structures and calculate physical properties as exemplified in the analysis of effective atomic charges in Sec. IV.

The structure of this paper is as follows: In Sec. II, we present the theory for calculating CWFs. Sec. III provides a detailed discussion on the implementation of the method. A series of benchmark calculations are presented in Sec. IV. Finally, in Sec. V, we summarize the theory of CWFs and suggest the potential role of CWFs as a foundation for developing novel methods.

II THEORY

Let us start by introducing Bloch functions $\{\varphi \}$, which can be obtained by solving the Kohn-Sham (KS) equation [25] within the density functional theory (DFT) [4], normalized as

$⟨{\varphi }_{{𝐤}_1\mu }|{\varphi }_{{𝐤}_2\nu }⟩=N_{\mathrm{BC}}{\delta }_{{𝐤}_1{𝐤}_2}{\delta }_{\mu \nu },$ (1)

where $𝐤$ and $\mu$ are the k-vector and band index, respectively, and $N_{\mathrm{BC}}$ is the number of primitive cells in the Born-von Karman (BvK) boundary condition. We consider the projection of a localized guiding function $Q$ onto the Bloch functions $\{\varphi \}$ weighted with a window function $w(\epsilon )$ as

$|L_{𝐑p}⟩={\displaystyle \frac{1}{N_{\mathrm{BC}}}}{\displaystyle \sum _{𝐤\mu }}{\mathrm{e}}^{-\mathrm{i}𝐤\cdot 𝐑}|{\varphi }_{𝐤\mu }⟩a_{𝐤\mu ,p}$ (2)

with

$a_{𝐤\mu ,p}=w({\epsilon }_{𝐤\mu })⟨{\varphi }_{𝐤\mu }|Q_{\mathrm{𝟎}p}⟩,$ (3)

where $𝐑$ and $p$ are the translational lattice vector and index of the localized orbital, respectively, ${\epsilon }_{𝐤\mu }$ is the eigenvalue of the KS equation, and $Q_{\mathrm{𝟎}p}\equiv Q_{𝐑p}$ $(𝐑=\mathrm{𝟎})$. In the summation of Eq. (2), the numbers of k-points and the Bloch functions to be included per k-point are $N_{\mathrm{BC}}$ and $N_{\mathrm{band}}$, respectively. Throughout this paper, we do not consider the spin dependency on the formulation for the sake of simplicity, but the generalization is straightforward. The localized functions $\{Q_{𝐑p}\}$, such as atomic orbitals, hybrid orbitals, or molecular orbitals (MOs), are assumed to localize in the unit cell specified by $𝐑$. When the window function $w(\epsilon )$ is taken to be unity, Eq. (2) is nothing but an expansion of $Q_{𝐑p}$ with Bloch functions from the identity relation $\frac{1}{N_{\mathrm{BC}}}{\sum }_{𝐤\mu }|{\varphi }_{𝐤\mu }⟩⟨{\varphi }_{𝐤\mu }|=\widehat{I}$. To introduce an expansion of $Q_{𝐑p}$ by the Bloch functions $\{{\varphi }_{𝐤\mu }\}$ in a subspace, we use the following window function $w(\epsilon )$:

$w(\epsilon )={\displaystyle \frac{1-\exp (x_0+x_1)}{(1+\exp (x_0))(1+\exp (x_1))}}+\delta$ (4)

with the definition of $x_0\equiv \beta ({\epsilon }_0-\epsilon )$ and $x_1\equiv \beta (\epsilon -{\epsilon }_1)$, where $\beta =\frac{1}{k_{\mathrm{B}}T}$ with the Boltzmann constant of $k_{\mathrm{B}}$ and a temperature of $T$. The window function of Eq. (4) is obtained by subtracting 1 from the sum of the two functions of $1/(1+\exp (x))$. It is also possible to introduce two temperatures $T_0$ and $T_1$. The usefulness of the two temperature scheme will be demonstrated for the case of GaAs in Sec. IV. The last term $\delta$ in Eq. (4) is a small constant, e.g., ${10}^{-12}$, which is introduced to avoid the ill-conditioning of the matrix consisting of $a_{𝐤\mu ,p}$ by Eq. (3) as will be discussed later. As shown in Fig. 1, the parameters of ${\epsilon }_0$ and ${\epsilon }_1$ () determine the energy range where the Bloch states are included in the expansion of Eq. (2) with a large weight, and the temperature $T$ provides the degree of smearing around ${\epsilon }_0$ and ${\epsilon }_1$ in $w(\epsilon )$. To control the degree of smearing, we introduce the temperature of $T$ so that one can intuitively understand the degree of smearing. It should be noted that the choice of the window function by Eq. (4) is not unique, and the other choices should give almost equivalent results as long as they are chosen properly. One may also consider that the window function has no special advantages over the outer and inner window scheme [8] and merely functions in a similar manner. However, the window function defined by Eq. (4) exhibits superior performance in the disentanglement of bands and calculation of effective charges. The advantages will be clearly demonstrated in Secs. IV A and IV B, respectively.

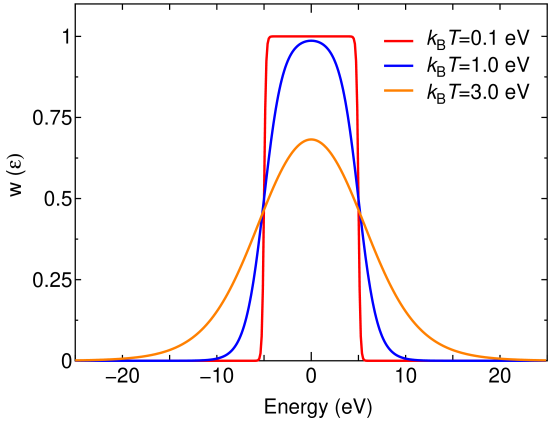
Figure 1: Window functions of Eq. (4) with $k_{\mathrm{B}}T$=0.1, 1.0, and 3.0 eV. ${\epsilon }_0$ and ${\epsilon }_1$ were set to be -5.0 and 5.0 eV, respectively, and $\delta ={10}^{-12}$ was used.

The function $L_{𝐑p}$ defined by Eq. (2) must be similar to the localized function $Q_{𝐑p}$, but they are generally non-orthogonal to each other. We now consider generating a set of closest Wannier functions (CWFs) $\{W_{𝐑p}\}$ to a set of localized functions $\{L_{𝐑p}\}$ in the sense that the sum of the squared distance between $L$ and $W$ in the Hilbert space is minimized. As well as Eq. (2), noting that the CWFs can be expressed [3] as

$|W_{𝐑p}⟩={\displaystyle \frac{1}{N_{\mathrm{BC}}}}{\displaystyle \sum _{𝐤\mu }}{\mathrm{e}}^{-\mathrm{i}𝐤\cdot 𝐑}|{\varphi }_{𝐤\mu }⟩b_{𝐤\mu ,p},$ (5)

and defining the residual function $R$:

$|R_{𝐑p}⟩=|L_{𝐑p}⟩-|W_{𝐑p}⟩,$ (6)

the distance measure (DM) function $F$ we minimize is given by

$F[B]$ $=$ ${\displaystyle \sum _p}⟨R_{\mathrm{𝟎}p}|R_{\mathrm{𝟎}p}⟩,$ (7)

$=$ ${\displaystyle \frac{1}{N_{\mathrm{BC}}}}{\displaystyle \sum _{𝐤}}X[B,𝐤]$

with

$X[B,𝐤]=\mathrm{tr}\left[\left(A^{†}(𝐤)-B^{†}(𝐤)\right)\left(A(𝐤)-B(𝐤)\right)\right],$ (8)

where the elements of the matrices $A(𝐤)$ and $B(𝐤)$ are given by $a_{𝐤\mu ,p}$ and $b_{𝐤\mu ,p}$, respectively. The second line of Eq. (7) is obtained by considering the orthonormality of Eq. (1), and $X[B,𝐤]$ of Eq. (8) is regarded as the squared Frobenius norm of $\left(A(𝐤)-B(𝐤)\right)$ [26]. The same Bloch functions as in Eq. (2) are included in the summation of Eq. (5). The number of CWFs to be generated is $N_{\mathrm{CWF}}$ per unit cell, being equivalent to the number of the guiding functions per cell, and $N_{\mathrm{CWF}}$ should be smaller than or equal to $N_{\mathrm{band}}$ to guarantee the linear independency of the subspace spanned by the CWFs, resulting in size of $N_{\mathrm{band}}\times N_{\mathrm{CWF}}$ for the matrices $A(𝐤)$ and $B(𝐤)$. Assuming $B^{†}(𝐤)B(𝐤)=I$, where $I$ is of size $N_{\mathrm{CWF}}\times N_{\mathrm{CWF}}$, the CWFs are ensured to form a set of orthonormal functions. Under this constraint, we consider the optimization of the DM function $F$. Furthermore, the matrix $B(𝐤)$ is regarded as a part of a unitary matrix of size $N_{\mathrm{band}}\times N_{\mathrm{band}}$, and will be referred to as a partial unitary matrix in subsequent discussions.

The minimum of the DM function of Eq. (7) is obtained by choosing $B(𝐤)$ as $U(𝐤)$ which is calculated by the polar decomposition of $A(𝐤)=U(𝐤)P(𝐤)$, where $U(𝐤)$ and $P(𝐤)$ are unitary and hermitian, respectively [27]. Let us prove the statement below. The polar decomposition of $A(𝐤)$ is obtained via SVD of $A(𝐤)$ as

$A=W\mathrm{\Sigma }{V}^{†}=W{V}^{†}V\mathrm{\Sigma }{V}^{†}=UP,$ (9)

where we dropped the dependency on $𝐤$ for simplicity of the notation, and hereafter we will denote the dependency if necessary. $W$ and $V$ are the left and right singular matrices in size of $N_{\mathrm{band}}\times N_{\mathrm{CWF}}$ and $N_{\mathrm{CWF}}\times N_{\mathrm{CWF}}$, respectively, and $\mathrm{\Sigma }$ is the singular value diagonal matrix in size of $N_{\mathrm{CWF}}\times N_{\mathrm{CWF}}$. Note that $U\equiv W{V}^{†}$ and $P\equiv V\mathrm{\Sigma }{V}^{†}$. It is worth mentioning that $W$ and $U$ are partial unitary matrices, and hold $W^{†}W=I$ ($W{W}^{†}\ne I$) and $U^{†}U=I$ ($U{U}^{†}\ne I$), and that $V$ is a full unitary matrix holding $V^{†}V=I$ ($V{V}^{†}=I$). We evaluate $X$ of Eq. (8) for each $𝐤$ with both the matrix $U$ obtained by the polar decomposition and an arbitrary partial unitary matrix $B$, and calculate the difference as

$X[U]-X[B]$ $=$ $2\mathrm{t}\mathrm{r}\left[{\displaystyle \frac{1}{2}}\left(A^{†}B+B^{†}A\right)-P\right],$ (10)

$=$ $2\mathrm{t}\mathrm{r}\left[\mathrm{\Sigma }D-\mathrm{\Sigma }\right],$

$=$ $2{\displaystyle \sum _n}{\sigma }_n\left(d_{nn}-1\right)$

with

$D={\displaystyle \frac{1}{2}}\left(V^{†}{U}^{†}BV+V^{†}{B}^{†}UV\right).$ (11)

The second line of Eq. (10) is derived by using the polar decomposition of $A$ and $P=V\mathrm{\Sigma }{V}^{†}$, and ${\sigma }_n$ and $d_{nn}$ in the third line are diagonal elements of $\mathrm{\Sigma }$ and $D$, respectively. The upper bound of the diagonal elements of the hermitian matrix $D$ is found to be unity, since the matrix $D$ consists of the sum of the product of partial unitary matrices of $V^{†}{U}^{†}$ ($V^{†}{B}^{†}$) and $BV$ ($UV$). Another proof for the upper bound is also given based on the Cauchy-Schwarz inequality in the appendix. By considering the upper bound of the diagonal elements of $D$ and $0\le {\sigma }_n$, the third line of Eq. (10) leads to the following inequality:

$X[U]\le X[B].$ (12)

The equality of Eq. (12) holds if $B=U$. If some of ${\sigma }_n$ is zero, the corresponding $d_{nn}$ in Eq. (10) can be arbitrarily chosen. So, we see from Eq. (11) that $U$ is not uniquely determined. If all the singular values of ${\sigma }_n$ are positive, all the $d_{nn}$s should be unity when $X[U]=X[B]$. The uniqueness of the solution can be confirmed as follows: Since the matrix $D$ consists of the products of the partial unitary matrices as discussed above, the case that all the diagonal elements $d_{nn}$ are unity happens when

$U^{†}B+B^{†}U=2I,$ (13)

which is derived by equating $D=I$ and multiplying $V$ and $V^{†}$ from the left and right of the equation, respectively. By noting again that $B$ and $U$ in Eq. (13) are the partial unitary matrices, it is found that Eq. (13) holds if and only if $B=U$. Thus, we have proven the statement that the minimum of the DM function of Eq. (7) is uniquely determined when $B=U$ as long as all the singular values of ${\sigma }_n$ are positive, since $F[B]$ of Eq. (7) consists of the sum of $X[B,𝐤]$ over k. The uniqueness of $U$ itself is related to that of the SVD for the matrix $A$ of Eq. (3). If $A$ has $N_{\mathrm{CWF}}$ positive singular values which are non-degenerate, the SVD is uniquely determined except for the non-unique phases in $W$ and $V$. Even if there are degenerate singular values, the matrix $U$ is invariant, since the freedom of the unitary transformation $K$ for the degenerate left and right singular vectors is canceled out as $U=WK{K}^{†}{V}^{†}=W{V}^{†}$ with $K{K}^{†}=I$. Further, noting that the non-unique phases in $W$ and $V$ are canceled out when the matrix $U$ is computed as $W{V}^{†}$, we conclude that $U$ is uniquely determined if $A$ has the $N_{\mathrm{CWF}}$ positive singular values. The violation from the positive definiteness of the singular values can be avoided by the small constant of $\delta$ in Eq. (4). On the other hand, if $\delta$ in Eq. (4) is set to be 0 and a narrow window, including fewer than $N_{\mathrm{CWF}}$ eigenstates for a given $𝐤$, is used with a small $k_{\mathrm{B}}T$, the matrix $A$ has $N_{\mathrm{PSV}}$ positive singular values, where . In this case, a subspace of the $\left(N_{\mathrm{CWF}}-N_{\mathrm{PSV}}\right)$ dimension is arbitrary chosen to form $W$ and $V$ of the dimension of $N_{\mathrm{CWF}}$ in addition to the subspace of the $N_{\mathrm{PSV}}$ dimension, which breaks the symmetry of CWFs. The symmetry breaking is due to the non-uniqueness of the SVD when some of the singular values are zero. The situation can be avoided by introducing a small constant $\delta$ in the window function of Eq. (4). The simple treatment restores the symmetry of CWFs, allowing us to calculate symmetry preserving CWFs for a wide variety of choices in the energy range of the window function. It is also noted that the non-unique phase of the Bloch functions is canceled out via the polar decomposition of $A$ and Eq. (5). We have the arbitrariness of phase both in calculating the Bloch functions and singular vectors $W$ and $V$, and unitary freedom $K$ for $W$ and $V$ when singular values are degenerate. However they are all canceled out as discussed above. Thus, we see that the proposed method is free from complications arising from the choice of gauge.

Using Eqs. (8) and (9), the minimum of the DM function $F$ at $B=U$ is given by

$F[U]={\displaystyle \frac{1}{N_{\mathrm{BC}}}}{\displaystyle \sum _{𝐤p}}{\left({\sigma }_{𝐤p}-1\right)}^2,$ (14)

where ${\sigma }_{𝐤p}$ is a singular value of the matrix $A(𝐤)$. From Eq. (14), we find that the mean squared distance between $L$ and $W$ is related to the deviation of $\sigma$ from unity.

The proposed method based on the polar decomposition of $A$ is closely related to the Löwdin orthogonalization [15] as shown below. The Fourier transform of the overlap integrals for $\{L\}$ is given by

${\displaystyle \sum _{𝐑}}{\mathrm{e}}^{\mathrm{i}𝐤\cdot 𝐑}⟨L_{\mathrm{𝟎}p}|L_{𝐑q}⟩={\displaystyle \sum _{\mu }}{a}_{𝐤\mu ,p}^{*}{a}_{𝐤\mu ,q},$ (15)

which is obtained by noting that $\frac{1}{N_{\mathrm{BC}}}{\sum }_{𝐑}{\mathrm{e}}^{\mathrm{i}(𝐤-{𝐤}^{\prime })\cdot 𝐑}={\delta }_{{\mathrm{𝐤𝐤}}^{\prime }}$. By writing Eq. (15) as $S(𝐤)=A^{†}(𝐤)A(𝐤)$ in a matrix form, and using Eq. (9), we have the following relation:

$S(𝐤)=A^{†}(𝐤)A(𝐤)=V^{†}(𝐤){\mathrm{\Sigma }}^2(𝐤)V(𝐤).$ (16)

Comparing Eq. (16) with $P(𝐤)=V(𝐤)\mathrm{\Sigma }(𝐤)V^{†}(𝐤)$, one obtains a relation $P(𝐤)=S^{1/2}(𝐤)$. If $P(𝐤)$ is invertible, the matrix $U(𝐤)$ is given with Eq. (9) by

$U(𝐤)=A(𝐤)S^{-1/2}(𝐤).$ (17)

The matrix $U$ obtained by Eq. (17) is exactly equivalent to that by the Löwdin orthogonalization [15], and the closest property of the Löwdin orthogonalized orbitals to a given set of orbitals was proven in Ref. [18]. On the other hand, the proposed method does not require the calculation of $S^{-1/2}$, and can be applied in a numerical stable manner even to the case that the matrix $A$ is nearly ill-conditioned. The definition of $A$ by Eq. (3) with the window function allows us to calculate CWFs in various respects, e.g., heavily weighting to occupied states and disentangling of localized states embedded in the wider bands as demonstrated in Sec. IV. In this sense, the method we propose can be regarded as a generalization of the Löwdin orthogonalization. We also notice that the projection method in Ref. [8] is equivalent to the proposed method in the sense that $U$ in Eq. (17) is calculated via the polar decomposition, and that the WFs obtained through the procedure [8] can be regarded as CWFs under the constraints of how the matrix $A$ is constructed.

The disentanglement of bands can be easily performed by properly selecting the window function of Eq. (3). Since the $N_{\mathrm{band}}(\ge N_{\mathrm{CWF}})$ Bloch functions per k-point are included in Eqs. (2) and (5), it should be emphasized that the proposed method always disentangles $N_{\mathrm{band}}$ states to generate $N_{\mathrm{CWF}}$ Wannier functions. A couple of examples will be shown in Sec. IV, including valence and low-lying conduction bands for the diamond Si and narrow $3d$-bands embedded in the wider $4s$-band for the face centered cubic (FCC) Cu.

Once the $k$-dependent $U(𝐤)$ are obtained by the polar decomposition, tight-binding (TB) parameters are calculated as expectation values of the KS Hamiltonian ${\widehat{H}}_{\mathrm{KS}}$ by summing contributions over $𝐤$ and $\mu$ as

$t_{\mathrm{𝟎}p,𝐑q}$ $=$ $⟨W_{\mathrm{𝟎}p}|{\widehat{H}}_{\mathrm{KS}}|W_{𝐑q}⟩,$ (18)

$=$ ${\displaystyle \frac{1}{N_{\mathrm{BC}}}}{\displaystyle \sum _{𝐤\mu }}{\epsilon }_{𝐤\mu }{u}_{𝐤\mu ,p}^{*}{u}_{𝐤\mu ,q}{\mathrm{e}}^{-\mathrm{i}𝐤\cdot 𝐑},$

where $u_{𝐤\mu ,q}$ is the matrix element of $U(𝐤)$. Like with MLWFs, the TB parameters can be used for the Wannier interpolation in calculations of band structures and physical quantities.

The computational procedure to generate the CWFs is summarized as follows:

1. Determining ${\epsilon }_0$, ${\epsilon }_1$, and $k_{\mathrm{B}}T$ in Eq. (4) by checking the band dispersion of a system of interest. The parameters should be chosen properly so that the targeted eigenstates can be included.

2. Choosing a set of localized orbitals {$Q$}. Atomic orbitals, hybrid orbitals, and MOs might be possible choices. Depending on the symmetry of the targeted eigenstates, a proper set of localized orbitals needs to be chosen, e.g., $d$-orbitals need to be employed in the generation of CWFs for the $d$-bands in FCC Cu as shown later on.

3. Calculation of $A(𝐤)$ by Eq. (3). The calculation of the overlap $⟨{\varphi }_{𝐤\mu }|Q_{\mathrm{𝟎}p}⟩$ depends on the implementation of the KS method.

4. Performing the SVD of $A(𝐤)$. A proper numerical library might be used.

5. Calculation of $U(𝐤)$. Using the left and right singular matrices, $W(𝐤)$ and $V(𝐤)$, of $A(𝐤)$, $U(𝐤)$ is calculated as $W(𝐤)V^{†}(𝐤)$.

6. Calculations of the CWFs and TB parameters. The CWFs can be calculated using Eq. (5) with $B=U$ obtained by the step 5. The calculation is expressed by the sum of the matrix-matrix product over $𝐤$. Also, the TB parameters are obtained by Eq. (18).

It should be stressed that the minimization of $F$ can be efficiently performed in a non-iterative manner by the steps 1 to 6 using the polar decomposition via the SVD. The computational cost of each step is estimated to be $O(N_{\mathrm{BC}}{N}_{\mathrm{band}}{N}_{\mathrm{CWF}}{N}_{\mathrm{basis}})$, $O(N_{\mathrm{BC}}{N}_{\mathrm{band}}^3)$, $O(N_{\mathrm{BC}}{N}_{\mathrm{band}}{N}_{\mathrm{CWF}}^2)$, or $O(N_{\mathrm{BC}}{N}_{\mathrm{band}}{N}_{\mathrm{CWF}}{N}_{\mathrm{basis}})$ for the step 3, 4, 5, or 6, respectively, where $N_{\mathrm{basis}}$ is the number of basis functions to expand the KS orbitals. If the localized basis functions are used, the computational cost of the step 3 becomes $O(N_{\mathrm{BC}}{N}_{\mathrm{band}}{N}_{\mathrm{CWF}})$.

For isolated systems, the Brillouin zone sampling is limited to only the $\mathrm{\Gamma }$ point. No modification of the proposed method is needed to calculate the CWFs.

The theoretical framework we have discussed so far is general for any implementation of the DFT-KS method. However, the choice of the the localized functions $\{Q\}$ in Eq. (3) may depend on the implementation. So, we will discuss how the localized functions $\{Q\}$ can be properly generated in Sec. III.

III IMPLEMENTATION

III.1 General

We have implemented the proposed method into the OpenMX DFT software package [28, 29, 30] which is based on norm-conserving pseudopotentials (PPs) [31, 32] and optimized pseudo-atomic orbitals (PAOs) [33, 34] as basis set. All the benchmark calculations were performed with a computational condition of a production level. The basis functions used are listed in Table 1. In the abbreviation of basis functions such as H7.0-s2p2d1, H stands for the atomic symbol, 7.0 the cutoff radius (Bohr) in the generation by the confinement scheme [33, 34], and s2p2d1 means the employment of two, two, and one optimized radial functions for the $s$-, $p$-, and $d$-orbitals, respectively. The radial functions were optimized by a variational optimization method [33]. These basis functions we used can be regarded as at least double zeta plus double polarization basis sets if we follow the terminology of Gaussian or Slater-type basis functions. Valence states included in the PPs are listed in Table 1. All the PPs and PAOs we used in the study were taken from the database (2019) in the OpenMX website [28], which were benchmarked by the delta gauge method [35]. Real space grid techniques were used for the numerical integrations and the solution of the Poisson equation using fast Fourier transform (FFT) with the energy cutoff of 250 to 500 Ryd [29]. We used a generalized gradient approximation (GGA) proposed by Perdew, Burke, and Ernzerhof to the exchange-correlation functional [36]. An electronic temperature of 300 K was used to count the number of electrons by the Fermi-Dirac function for all the systems we considered. For all the calculations, $\delta ={10}^{-12}$ was used in the window function of Eq. (4), and $N_{\mathrm{band}}$ was set to be equivalent to the number of basis functions in both the summation of Eqs. (2) and (5).

Table 1: Basis functions and valence states included in PPs. ${}^{*}$For the calculations of atomic charges, the basis functions listed in Table III were used.

Element	Basis functions	Valence states in PP
H	${}^{*}$H7.0-s2p2d1	$1s$
C	${}^{*}$C6.0-s3p2d2	$2s$, $2p$
N	${}^{*}$N6.0-s3p2d2	$2s$, $2p$
Na	${}^{*}$Na9.0-s3p3d2f2	$2s$, $2p$, $3s$
Si	Si7.0-s2p2d2f1	$3s$, $3p$
Cl	${}^{*}$Cl9.0-s3p3d2f2	$3s$, $3p$
S	S7.0-s3p2d2f1	$3s$, $3p$
Cu	Cu6.0-s3p3d3f1	$3s$, $3p$, $3d$, $4s$
Ga	Ga7.0-s3p2d2f1	$3d$, $4s$, $4p$
As	As7.0-s3p2d2f1	$3d$, $4s$, $4p$
Se	Se7.0-s3p2d2	$4s$, $4p$
Bi	Bi8.0-s3p2d2f1	$5d$, $6s$, $6p$

III.2 Choice of Guiding Functions $\{Q\}$

Depending on the targeted eigenstates in the window function of Eq. (4), one can choose either atomic orbitals, hybrid atomic orbitals, or MOs as the guiding functions $\{Q\}$ in Eq. (3). In this subsection we discuss the three kinds of the localized guiding functions $\{Q\}$, i.e., atomic orbitals, hybrid atomic orbitals, and embedded MOs in molecules and bulks, and how they can be generated in our implementation.

In our implementation, the Bloch function ${\varphi }_{𝐤\mu }$ is expanded by PAOs $\chi$ [33, 34] as

$|{\varphi }_{𝐤\mu }⟩={\displaystyle \sum _{𝐑}}{\mathrm{e}}^{\mathrm{i}𝐤\cdot 𝐑}{\displaystyle \sum _{i\alpha }}{c}_{𝐤\mu ,i\alpha }|{\chi }_{𝐑i\alpha }⟩,$ (19)

where $i$ and $\alpha$ are atomic and orbital indices, and $c$ is a linear combination of PAO (LCPAO) coefficient. Also note that $⟨𝐫|{\chi }_{𝐑i\alpha }⟩\equiv {\chi }_{i\alpha }(𝐫-{\tau }_i-𝐑)$, where ${\tau }_i$ is the position of atom $i$. We use PAOs as the guiding functions $\{Q\}$ of atomic orbitals, corresponding to valence orbitals or specific orbitals such as localized $d$-orbitals in a narrow energy window.

The choice of the atomic orbitals gives a good guiding function, however, the resultant CWFs may not recover the symmetry of CWFs respecting the bond direction to the neighboring atoms unlike hybrid atomic orbitals due to the closest property of CWFs. In this case, it would be better to use the hybrid atomic orbitals rather than the atomic orbitals as explained below. Let us introduce a projection operator for the occupied space by

$\widehat{P}={\displaystyle \frac{1}{N_{\mathrm{BC}}}}{\displaystyle \sum _{𝐤\mu }}|{\varphi }_{𝐤\mu }⟩f({\epsilon }_{𝐤\mu })⟨{\varphi }_{𝐤\mu }|,$ (20)

where $f$ is the Fermi-Dirac function. Considering that $\{\chi \}$ are a set of non-orthogonal basis set [37], where the overlap integral is denoted by $s_{𝐑i\alpha ,{𝐑}^{\prime }j\beta }\equiv ⟨{\chi }_{𝐑i\alpha }|{\chi }_{{𝐑}^{\prime }j\beta }⟩$, the density matrix is calculated with the projection operator by

${\rho }_{𝐑i\alpha ,{𝐑}^{\prime }j\beta }$ $=$ ${\displaystyle \sum _{𝐤\mu }}⟨{\tilde{\chi }}_{𝐑i\alpha }|\widehat{P}|{\tilde{\chi }}_{{𝐑}^{\prime }j\beta }⟩,$ (21)

$=$ ${\displaystyle \frac{1}{N_{\mathrm{BC}}}}{\displaystyle \sum _{𝐤\mu }}{\mathrm{e}}^{\mathrm{i}𝐤\cdot \left(𝐑-{𝐑}^{\prime }\right)}f({\epsilon }_{𝐤\mu })c_{𝐤\mu ,i\alpha }{c}_{𝐤\mu ,j\beta }^{*},$

where $\tilde{\chi }$ is the dual orbital defined by

$|{\tilde{\chi }}_{𝐑i\alpha }⟩$ $=$ ${\displaystyle \sum _{{𝐑}^{\prime }j\beta }}|{\chi }_{{𝐑}^{\prime }j\beta }⟩s_{{𝐑}^{\prime }j\beta ,𝐑i\alpha }^{-1}$ (22)

holding the following orthonormality:

$⟨{\chi }_{𝐑i\alpha }|{\tilde{\chi }}_{{𝐑}^{\prime }j\beta }⟩$ $=$ $⟨{\tilde{\chi }}_{𝐑i\alpha }|{\chi }_{{𝐑}^{\prime }j\beta }⟩={\delta }_{{\mathrm{𝐑𝐑}}^{\prime }}{\delta }_{ij}{\delta }_{\alpha \beta }.$ (23)

By setting $𝐑={𝐑}^{\prime }=\mathrm{𝟎}$ and $i=j$ in Eq. (21), and diagonalizing the diagonal block element consisting of ${\rho }_{\mathrm{𝟎}i\alpha ,\mathrm{𝟎}i\beta }$, which is associated with selected atomic orbitals on the atomic site $i$, we obtain the hybrid atomic orbitals respecting the symmetry of the bond direction to the neighboring atoms. We employ the hybrid atomic orbitals as the localized functions $\{Q\}$ in our implementation. When the same atomic orbitals are chosen to form the diagonal block element as for the case of atomic orbitals $\{Q\}$, the resultant CWFs span the same subspace in the Hilbert space.

For some systems the electronic structures can be rather easily understood by employing MOs as building blocks. A molecular crystal is such a case, where the eigenstates near the chemical potential can be approximately constructed by a linear combination of the MOs of constituting molecules. Another example is the bond in molecules and bulks. The bond between two atoms embedded in the system might be analyzed by MOs associated with the two atoms. Here we show how embedded MOs in molecules and bulks can be calculated in a simple procedure. Let us start by noting that using Eq. (20) and assuming that the Bloch function is expressed by Eq. (19) the total number of electrons for a spin degenerate case is given by [37]

$N_{\mathrm{ele}}$ $=$ $2\mathrm{t}\mathrm{r}\left[\widehat{P}\right],$ (24)

$=$ $2{\displaystyle \sum _{𝐑i\alpha }}⟨{\tilde{\chi }}_{𝐑i\alpha }|\widehat{P}|{\chi }_{𝐑i\alpha }⟩,$

In the second line of Eq. (24) we used the following identity operator:

$\widehat{I}={\displaystyle \sum _{𝐑i\alpha }}|{\chi }_{𝐑i\alpha }⟩⟨{\tilde{\chi }}_{𝐑i\alpha }|={\displaystyle \sum _{𝐑i\alpha }}|{\tilde{\chi }}_{𝐑i\alpha }⟩⟨{\chi }_{𝐑i\alpha }|.$ (25)

Since $N_{\mathrm{ele}}=N_{\mathrm{BC}}{N}_{\mathrm{ele}}^{(0)}$ with $N_{\mathrm{ele}}^{(0)}=2{\sum }_{i\alpha }⟨{\tilde{\chi }}_{\mathrm{𝟎}i\alpha }|\widehat{P}|{\chi }_{\mathrm{𝟎}i\alpha }⟩$, it is enough to consider $N_{\mathrm{ele}}^{(0)}$. We utilize the formula for $N_{\mathrm{ele}}^{(0)}$ to calculate embedded MOs in molecules and bulks, and rewrite it the sum of partial traces as

$N_{\mathrm{ele}}^{(0)}=2{\displaystyle \sum _g}{\mathrm{tr}}_g\left[({\tilde{\chi }}_{\mathrm{𝟎}g}|\widehat{P}|{\chi }_{\mathrm{𝟎}g})\right]=2{\displaystyle \sum _g}{\mathrm{tr}}_g\left[{\mathrm{\Lambda }}_g\right],$ (26)

where $g$ is the index of group including PAOs on grouped atoms, e.g., a set of PAOs on a molecule. The notation of $|{\chi }_{\mathrm{𝟎}g})$ stands for a subset of PAOs as

$|{\chi }_{\mathrm{𝟎}g})=(\mathrm{\cdots },|{\chi }_{\mathrm{𝟎}i1}⟩,|{\chi }_{\mathrm{𝟎}i2}⟩,\mathrm{\cdots },),$ (27)

where PAOs on all the atoms in the group $g$ are included in the subset. The notation of $|{\tilde{\chi }}_{\mathrm{𝟎}g})$ is the counterpart for the dual orbitals. Using the identity operator of Eq. (25), ${\mathrm{\Lambda }}_g$ in Eq. (26) is given by

${\mathrm{\Lambda }}_g={\displaystyle \sum _{𝐑g^{\prime }}}{\rho }_{\mathrm{𝟎}g,𝐑g^{\prime }}{s}_{𝐑g^{\prime },\mathrm{𝟎}g}$ (28)

with definition of block elements:

${\rho }_{𝐑g,{𝐑}^{\prime }{g}^{\prime }}$ $=$ $({\tilde{\chi }}_{𝐑g}|\widehat{P}|{\tilde{\chi }}_{{𝐑}^{\prime }{g}^{\prime }}),$ (29)

$s_{𝐑g,{𝐑}^{\prime }{g}^{\prime }}$ $=$ $({\chi }_{𝐑g}|{\chi }_{{𝐑}^{\prime }{g}^{\prime }}).$ (30)

We now introduce the embedded MOs orbitals in molecules and bulks by a right-singular vectors of ${\mathrm{\Lambda }}_g$ [38]. Since the elements of ${\mathrm{\Lambda }}_g$ are real in case of the collinear DFT, the right-singular vectors can be obtained with real components. However, the SVD of ${\mathrm{\Lambda }}_g$ tends to produce the right-singular vectors with complex components, which results in the complex CWFs making analysis complicated. To obtain the real right-singular vectors, we perform the eigendecomposition of ${\mathrm{\Lambda }}_g^{†}{\mathrm{\Lambda }}_g$ as

${\mathrm{\Lambda }}_g^{†}{\mathrm{\Lambda }}_g=Y_g{\mathrm{\Omega }}_g^2{Y}_g^{†},$ (31)

where ${\mathrm{\Omega }}_g^2$ is the diagonal matrix consisting of the eigenvalues of ${\mathrm{\Lambda }}_g^{†}{\mathrm{\Lambda }}_g$, and $Y_g$ is a unitary matrix consisting of the corresponding eigenvectors $\{y_{g,\nu }\}$. By noting that the SVD of ${\mathrm{\Lambda }}_g$ is given by $Z_g{\mathrm{\Omega }}_g{Y}_g^{†}$, we see that the right-singular vectors $Y_g$ can be obtained by diagonalizing ${\mathrm{\Lambda }}_g^{†}{\mathrm{\Lambda }}_g$ as $Y_g$. The square roots of the eigenvalues of ${\mathrm{\Lambda }}_g^{†}{\mathrm{\Lambda }}_g$ are singular values of ${\mathrm{\Lambda }}_g$, and can be approximately regarded as the occupation of the corresponding eigenvector $y_{g,\nu }$. If ${\mathrm{\Lambda }}_g$ is a real matrix, $Y_g$ obtained by the diagonalization of ${\mathrm{\Lambda }}_g^{†}{\mathrm{\Lambda }}_g$ is guaranteed to be a real unitary matrix. We further normalize the eigenvector $y_{g,\nu }$ by considering the overlap integrals of Eq. (30) as

$|{\overline{y}}_{g,\nu }⟩={\displaystyle \frac{|y_{g,\nu }⟩}{\sqrt{⟨y_{g,\nu }|s_{\mathrm{𝟎}g,\mathrm{𝟎}g}|y_{g,\nu }⟩}}},$ (32)

and calculate an expectation value of the KS Hamiltonian ${\widehat{H}}_{\mathrm{KS}}$ with ${\overline{y}}_{g,\nu }$ as

${ϵ}_{g,\nu }=⟨{\overline{y}}_{g,\nu }|{\widehat{H}}_{\mathrm{KS}}|{\overline{y}}_{g,\nu }⟩.$ (33)

After $\{{\overline{y}}_{g,\nu }\}$ are ordered based on the expectation values, we employ selected ones among $\{{\overline{y}}_{g,\nu }\}$, e.g., ones near the chemical potential, as the guiding functions $\{Q\}$ in Eq. (3) by monitoring the expectation values and the corresponding singular values. They are what we call embedded MOs in molecules and bulks. The reason why the expectation values are used to select the embedded MOs in addition to the singular values is that the singular values are found to be almost similar to each other as long as they are associated with occupied states. As demonstrated in Sec. IV, $\{\overline{y}\}$ work as the good guiding functions to capture the electronic structure of a molecular crystal.

IV NUMERICAL RESULTS

IV.1 Wannier Interpolated Bands

We present five numerical examples to demonstrate the broad applicability of the proposed method across various systems. In addition, a series of benchmark calculations for 30 systems are shown as supplementary information on a website [39]. In Figs. 2 (a) and (b), the interpolated bands of Si in the diamond structure, calculated by the TB Hamiltonian derived from CWFs, are compared with those by the conventional calculation. For comparison, the result with the projection-only WFs is also shown in Fig. 2 (c), calculated by the projection method in Ref. [8]. The hybrid atomic orbitals consisting of valence minimal orbitals, which are one $s$- and a set of $p_x$-, $p_y$-, and $p_z$-orbitals per Si, were used as the guiding functions $\{Q\}$. For the window function of Eq. (4) we use -15.0 and 0.0, relative to the chemical potential, in eV for ${\epsilon }_0$ and ${\epsilon }_1$, respectively, which covers the energy range of valence bands. On the other hand, two $k_{\mathrm{B}}T$ of 0.01 and 3.0 eV were used to check how conduction bands are reproduced depending on the effect of smearing. As clearly seen, the two cases well reproduce the valence bands, and the conduction bands are also reproduced well in the case (b) of $k_{\mathrm{B}}T=3.0$ eV. We also note that the interpolated bands by the projection-only WFs reproduce well the reference as shown in Fig. 2 (c). Evaluating the DM function per CWF using Eq. (14), we obtain values of 0.571 and 0.444 for $k_{\mathrm{B}}T$ of 0.01 and 3.0 eV, respectively. For $k_{\mathrm{B}}T=0.01$ eV, the first four singular values at each $k$ point are close to 1, while the remaining four approach $\delta (={10}^{-12})$. Conversely, for $k_{\mathrm{B}}T=3.0$ eV, the eight singular values at each $k$ point distribute ranging from 1.2 to 0.1. These differences in the distribution of singular values explain why the value of the DM function for $k_{\mathrm{B}}T=0.01$ eV is larger than that for $k_{\mathrm{B}}T=3.0$ eV. One of the obtained CWFs is shown in Fig. 2 (d), which represents a $p$-like CWF. Although the proposed method does not impose the localization of WFs, the decaying property of TB parameters $t$ exhibits a subexponential behavior as shown in Fig. 2 (e). In case of $k_{\mathrm{B}}T=0.01$ eV, the conduction bands are treated less importantly due to heavily weighting to the valence bands, resulting in the poor reproduction of the conduction bands. At first glance, one may consider that this is an undesirable feature in such a treatment. However, the feature enables us to generate the minimal atomic-like orthogonal orbitals, which well span the subspace by the valence bands, and to calculate an effective charge allocated to each atom using the minimal atomic-like orthogonal orbitals in an unbiased way. We will demonstrate the calculation of the effective atomic charges and stress the usefulness of the method later on.

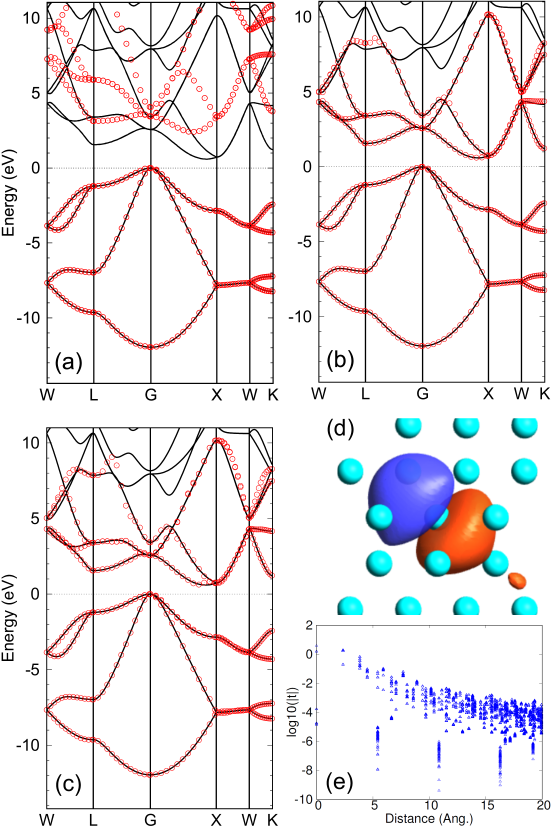
Figure 2: Interpolated bands (red circles) of silicon in the diamond structure, calculated by the TB Hamiltonian derived from CWFs with (a) $k_{\mathrm{B}}T$=0.01 and (b) 3.0 eV in the window function of Eq. (4), respectively. ${\epsilon }_0$ and ${\epsilon }_1$ relative to the chemical potential were set to be -15.0 and 0.0 eV, respectively. The solid line is the original one directly calculated by the conventional scheme. The result with the projection-only WFs is shown in (c), calculated by the projection method in Ref. [8] with the outer window (-14.0 to 11.0 eV) and the inner window (-14.0 to 5.0 eV). The number of k-points for the Brillouin zone sampling was 13 $\times$ 13 $\times$ 13. The experimental lattice constant of 5.43 Å was used. The values of the DM function per CWF are 0.571 and 0.444 for (a) and (b), respectively. (d) a CWF in the case (b), where isovalues of $\pm 0.04$ (orange:0.04, blue:-0.04) were used for drawing the isosurfaces using OpenMX Viewer [40]. The same isovalues were used for the cases of Figs. 3(d), 4(c), and 4(d). (e) TB parameters $t$ (eV) for the case (a) as a function of distance.

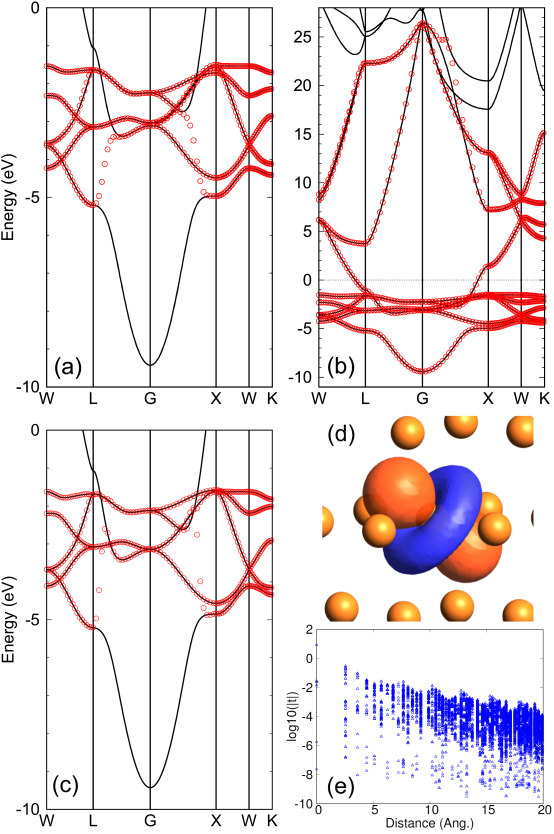
Figure 3: Interpolated bands (red circles) of copper in the FCC structure, calculated by the TB Hamiltonian derived from CWFs with (a) ${\epsilon }_0=-5.5$, ${\epsilon }_1=-1.0$ eV, $k_{\mathrm{B}}T=1.0$ eV, and hybrid $3d$-orbitals as $\{Q\}$, and (b) ${\epsilon }_0=-11.0$, ${\epsilon }_1=24.0$ eV, $k_{\mathrm{B}}T=3.0$ eV, and hybrid $3d$-, $4s$-, $4p$-orbitals as $\{Q\}$. The solid line is the original one directly calculated by the conventional scheme. The result with the projection-only WFs calculated with the same guiding functions in (b) is shown in (c), for which the projection method in Ref. [8] was used with the outer window (-10.0 to 0.0 eV) and the inner window (-4.0 to -2.0 eV). The number of k-points for the Brillouin zone sampling was 21 $\times$ 21 $\times$ 21. The experimental lattice constant of 3.61 Å was used. The values of the DM function per CWF are 0.081 and 0.211 for (a) and (b), respectively. (d) a CWF in the case (a). (e) TB parameters $t$ (eV) for the case (a) as a function of distance.

The disentanglement of bands in metals is demonstrated for Cu in the FCC structure as shown in Figs. 3 (a) and (b). For comparison, the result with the projection-only WFs is also shown in Fig. 3 (c). By selecting the parameters ${\epsilon }_0$ and ${\epsilon }_1$ so that the $3d$ bands are included, and using only five $d$-orbitals as the guiding functions $\{Q\}$, the five $d$-bands are reproduced as shown in Fig. 3 (a). We see that the $3d$-bands are properly disentangled from the dispersive $4s$ band, and one of the obtained CWFs preserves the shape of $d_{z^2}$-orbital as shown in Fig. 3 (d) in accordance with the subexponential decaying property of the TB parameters as shown in Fig. 3 (e). When $3d$-, $4s$-, and $4p$-orbitals are used as the guiding functions $\{Q\}$, a broad range of bands are reproduced as shown in Fig. 3 (b). Since our PP of Cu includes $3s$, $3p$, $3d$, and $4s$ states, the original band structure has the deep $3s$- and $3p$-bands. We set the parameters in the window function so as to discard the $3s$- and $3p$-bands, and use the $3d$-, $4s$-, and $4p$-orbitals, not $3s$- and $3p$-orbitals, as the guiding functions $\{Q\}$. So, the $3s$- and $3p$-bands are not included in the interpolated bands (not shown). The examples show that the CWFs can be flexibly and easily constructed in accordance with the purpose of study without numerical difficulties. On the other hand, the interpolated bands by the projection-only Wannier functions (WFs) demonstrate good agreement with the reference, as shown in Fig. 3 (c). This agreement is achieved through the minimization of ${\mathrm{\Omega }}_{\mathrm{I}}$, which is originally called gauge invariant part of the spread function $\mathrm{\Omega }$, as discussed in Ref. [8]. Without minimizing ${\mathrm{\Omega }}_{\mathrm{I}}$, however, the bands obtained by the projection-only WFs lose smoothness and exhibit slight deviations from the reference (not shown) as discussed in Ref. [3]. Our method achieves good agreement with the reference without any iterative calculations, as illustrated in Fig. 3 (a). This remarkable property can be attributed to the use of the smoothly varying window function of Eq. (4).

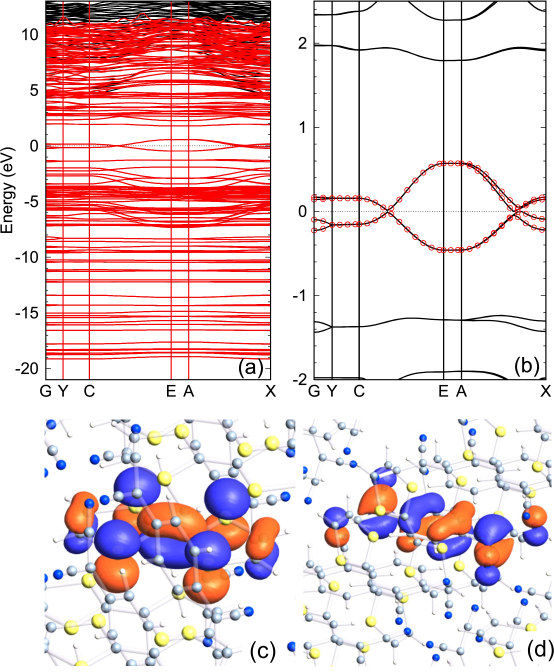
Figure 4: Interpolated bands, red lines in (a) and red circles in (b), of TTF-TCNQ, calculated by the TB Hamiltonian derived from CWFs with (a) ${\epsilon }_0=-22.0$ and ${\epsilon }_1=1.0$ eV relative to the chemical potential, $k_{\mathrm{B}}T=2.0$ eV, and hybrid atomic valence orbitals as $\{Q\}$, and (b) ${\epsilon }_0=-1.0$ and ${\epsilon }_1=1.0$ eV relative to the chemical potential, $k_{\mathrm{B}}T=0.01$ eV, and the 26th MO and the 37th MO for TTF and TCNQ as $\{Q\}$. The solid line is the original one directly calculated by the conventional scheme. The number of k-points for the Brillouin zone sampling was 5 $\times$ 19 $\times$ 3. An experimental crystal structure was used [41]. The values of the DM function per CWF are 0.441 and 0.022 for (a) and (b), respectively. CWFs for (c) TTF in TTF-TCNQ, and (d) TCNQ in TTF-TCNQ, obtained from the case (b).

The interpolated bands for a molecular crystal, consisting of tetrathiafulvalene (TTF) and tetracyanoquinodimethane (TCNQ), are shown in Figs. 4 (a) and (b). By employing hybrid atomic orbitals as the guiding functions $\{Q\}$, the wide range of bands are reproduced as shown in Fig. 4 (a). On the other hand, as shown in Fig. 4 (b), only four bands near the chemical potential are reproduced using the embedded MOs in the bulk as the guiding functions $\{Q\}$. The MOs were calculated by grouping the TTF and TCNQ molecules separately as explained in Sec. III B. The expectation values calculated by Eq. (33) and the singular values $\omega$ of ${\mathrm{\Lambda }}_g$ are listed in Table 2. It can be seen that the singular values largely change from ${\omega }_{26}$ to ${\omega }_{27}$ and from ${\omega }_{37}$ to ${\omega }_{38}$ for TTF and TCNQ, respectively. So, the 26th MO and the 37th MO for TTF and TCNQ, respectively, were used as the guiding functions $\{Q\}$. Since there are two TTF molecules and two TCNQ molecules in the unit cell, we have the four embedded MOs as $\{Q\}$, resulting in the four bands. In Figs. 4 (c) and (d) two of the resultant CWFs are shown, which localize in TTF and TCNQ molecules, respectively, as expected. The value of the DM function per CWF is found to be 0.022, which implies that the guiding MOs are very close to the resultant CWFs. The example demonstrates that the proposed method provides a direct way to calculate CWFs for targeted bands in molecular crystals.

Table 2: Expectation values $ϵ$ (eV) of the KS Hamiltonian calculated by Eq. (33), which is relative to the chemical potential, and singular values $\omega$ of ${\mathrm{\Lambda }}_g$ for embedded MOs in the TTF-TCNQ molecular crystal.

	TTF			TCNQ
index	$ϵ$	$\omega$	index	$ϵ$	$\omega$
23	-0.069	1.359	34	0.135	1.082
24	0.719	1.346	35	0.375	1.329
25	0.761	1.449	36	0.477	1.336
26	3.408	0.864	37	4.928	0.535
27	5.947	0.047	38	9.389	0.036
28	6.197	0.047	39	9.795	0.019

We extend the proposed method to the non-collinear DFT [42, 43] with spin-orbit interaction (SOI) [32]. The KS orbitals are expressed by two-component spinor, and the SOI is introduced by fully relativistic $j$-dependent PPs [28]. The theoretical framework is readily extended to the non-collinear DFT with the SOI without any difficulty. However, it should be noted that the hybrid atomic orbitals and embedded MOs in molecules and bulks as the guiding functions $\{Q\}$ can be complex functions in the case. In Figs. 5 (a) and (b), we show the Wannier interpolated bands of Bi${}_2$Se${}_3$ which is known to be a topological insulator when the SOI is included in the DFT calculation. For the cases without and with the SOI, corresponding to Figs. 5 (a) and (b), respectively, it is confirmed that the interpolated bands accurately reproduce the original ones regardless of existence of the band inversion, demonstrating a wide variety of applicability of the proposed method.

Figure 5: Interpolated bands (red circles) of Bi${}_2$Se${}_3$ (a) without and (b) with the spin-orbit interaction, calculated by the TB Hamiltonian derived from CWFs. The solid line is the original ones directly calculated by the conventional scheme. ${\epsilon }_0=-6.0$ and ${\epsilon }_1=3.0$ eV relative to the chemical potential, $k_{\mathrm{B}}T=1.0$ eV, and hybrid Bi $6p$-orbitals and Se $4p$-orbitals as $\{Q\}$, were used in both the calculations. The number of k-points for the Brillouin zone sampling was 7 $\times$ 7 $\times$ 7. An experimental crystal structure was used [44]. The values of the DM function per CWF are 0.163 and 0.184 for (a) and (b), respectively.

Finally, we show results for GaAs in Figs. 6 (a)-(d) to demonstrate how the window function of Eq. (4) with the two temperature scheme plays a significant role in reproducing the targeted bands. The interpolated bands calculated with the projection-only WFs calculated by the projection method in Ref. [8] reproduce well the reference ones as shown in Fig. 6 (a). When the four bands located just below the chemical potential, which mainly consists of Ga-$4s$ and As-$4p$ orbitals, are focused by discarding the other bands with $k_{\mathrm{B}}{T}_0=k_{\mathrm{B}}{T}_1$ = 0.001 eV, interpolated bands are obtained as shown in Fig. 6 (b). Other the other hand, including outer bands with $k_{\mathrm{B}}{T}_0=k_{\mathrm{B}}{T}_1$ = 1.0 eV leads to an erratic behavior as shown in Fig. 6 (c), where the CWFs attempt to reproduce the lower band located around -12 eV and low lying unoccupied bands depending on the k-point, resulting in the erratic behavior. Noting that the three bands in between -7 and 0 eV consists of mainly Ga-$4s$ and As-$4p$ orbitals and the low lying unoccupied bands are largely contributed by Ga-$4p$ orbitals, the band around -12 eV needs to be completely discarded and the low lying unoccupied bands should be partly included when Ga-$4s$, $4p$, and As-$4p$ orbitals are used as the guiding functions. The result in Fig. 6 (d) is the case, where $k_{\mathrm{B}}{T}_0$ = 0.001 and $k_{\mathrm{B}}{T}_1$ = 1.0 eV were used. We see that the interpolated bands fully reproduce the reference ones as expected, which clearly demonstrates the usefulness of the two temperature scheme.

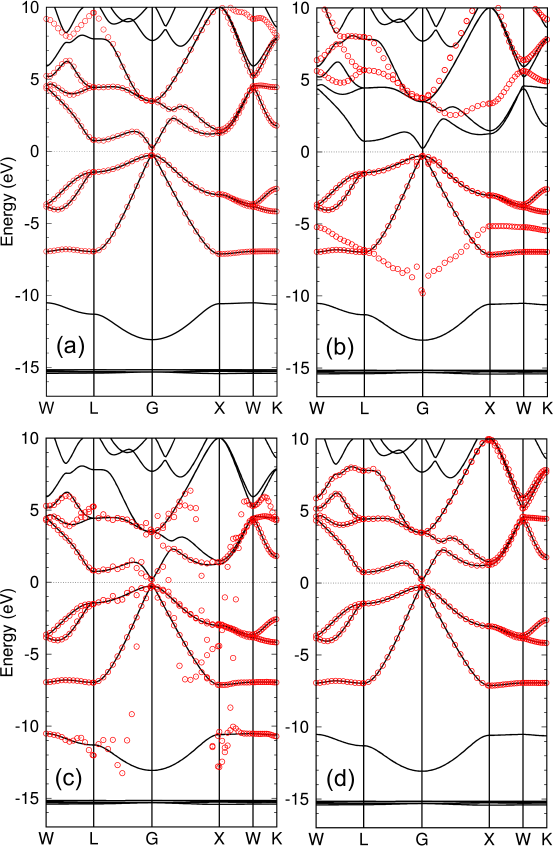
Figure 6: Interpolated bands (red circles) of GaAs in the zinc blende structure, calculated by the TB Hamiltonian derived from (a) projection-only WFs calculated by the projection method in Ref. [8] with the outer window (-10.0 to 12.0 eV) and the inner window (-8.0 to 6.0 eV), CWFs with (b) $k_{\mathrm{B}}{T}_0=k_{\mathrm{B}}{T}_1$ = 0.001 eV, (c) $k_{\mathrm{B}}{T}_0=k_{\mathrm{B}}{T}_1$ = 1.0 eV, and (d) $k_{\mathrm{B}}{T}_0$ = 0.001 and $k_{\mathrm{B}}{T}_1$ = 1.0 eV, respectively. For (b), (c), and (d), ${\epsilon }_0$ and ${\epsilon }_1$ relative to the chemical potential were set to be -9.0 and 0.0 eV, respectively. Ga-$4s$, $4p$, and As-$4p$ orbitals were used as the guiding functions in all the cases. The solid line is the original one directly calculated by the conventional scheme. The number of k-points for the Brillouin zone sampling was 13 $\times$ 13 $\times$ 13. The experimental lattice constant of 5.65 Å was used. The value of the DM function per CWF is 0.578 in the case (d).

IV.2 Effective Atomic Charges

From the construction, one can calculate CWFs closest to (hybrid) valence atomic orbitals, while fully respecting the occupied states. The feature of CWFs provides us a unique way to evaluate effective atomic charges based on CWFs being orthogonal atomic-like orbitals. Since the CWFs are a set of orthonormal functions, the effective atomic charge ${\kappa }_i$ of atom $i$ is easily calculated without arbitrariness as

${\kappa }_i$ $=$ $N_i^{(\mathrm{val})}-2{\displaystyle \sum _{p\in \mathrm{atom}\mathrm{\_}i}}⟨W_{\mathrm{𝟎}p}|\widehat{P}|W_{\mathrm{𝟎}p}⟩,$ (34)

$=$ $N_i^{(\mathrm{val})}-{\displaystyle \frac{2}{N_{\mathrm{BC}}}}{\displaystyle \sum _{p\in \mathrm{atom}\mathrm{\_}i}}{\displaystyle \sum _{𝐤,\mu }}f({\epsilon }_{𝐤\mu })u_{𝐤\mu ,p}^{*}{u}_{𝐤\mu ,p},$

where the factor of 2 is due to the spin degeneracy, $\widehat{P}$ is the projection operator defined by Eq. (20), and $N_i^{(\mathrm{val})}$ is the number of valence electrons in the PP of atom $i$. Though the summation over orbitals $p$ belonging to atom $i$ is taken into account in Eq. (34), one can analyze the orbital resolved charges as well. Table III shows effective atomic charges in a HCN molecule and the NaCl bulk, calculated by Eq. (34) together with effective charges calculated by MLWFs [3, 7], the projection-only WFs (POWF) [8], the Mulliken population analysis [45], and the Bader analysis [46, 47].

Table 3: Effective atomic charges in a HCN molecule and the NaCl bulk, calculated by the proposed method (CWF), the MLWFs (MLWF), the projection-only WFs (POWF) [8], the Mulliken population analysis (MP), and the Bader analysis (Bader) with a variety of basis functions, where $A$ represents the constituting atoms. Valence atomic orbitals were used as the guiding functions $\{Q\}$. For the window function, ${\epsilon }_0=-55.0$ and ${\epsilon }_1=0.0$ eV for HCN and ${\epsilon }_0=-35.0$ and ${\epsilon }_1=0.0$ eV for NaCl, relative to the chemical potential, and $k_{\mathrm{B}}T=0.1$ eV are used. The same number of MLWFs and POWFs as the cases of CWF were generated starting from the same valence atomic orbitals as the initial guess, where the outer and inner windows, relative to the chemical potential, were set to be -22.0 to 14.0 (-30.0 to 37.0) and -22.0 to 0.0 (-29.0 to 0.0) eV for HCN (NaCl), respectively. The number of k-points for the Brillouin zone sampling is 9 $\times$ 9 $\times$ 9 for the NaCl bulk with the lattice constant of 5.63 Å.

HCN		CWF			MLWF			POWF			MP			Bader
Basis	H	C	N	H	C	N	H	C	N	H	C	N	H	C	N
$A$6.0-s1p1	0.077	-0.052	-0.025	0.665	0.303	-0.969	0.262	-0.215	-0.047	0.384	-0.164	-0.221	1.000	1.746	-2.746
$A$6.0-s2p2	0.069	0.003	-0.073	0.793	0.067	-0.860	0.312	-0.009	-0.303	-0.070	0.321	-0.252	0.201	2.439	-2.639
$A$6.0-s2p2d1	0.066	0.009	-0.076	0.793	0.102	-0.907	0.307	0.010	-0.317	-0.008	0.393	-0.385	0.183	2.523	-2.706
$A$6.0-s3p3d2	0.066	0.008	-0.074	0.699	0.343	-1.042	0.314	0.001	-0.315	0.110	0.298	-0.408	0.182	2.539	-2.721
$A$6.0-s3p3d2f2	0.066	0.008	-0.074	0.721	0.344	-1.065	0.308	0.007	-0.315	0.167	0.297	-0.464	0.182	2.532	-2.715
NaCl	CWF			MLWF			POWF			MP			Bader
Basis	Na	Cl		Na	Cl		Na	Cl		Na	Cl		Na	Cl
$A$9.0-s2p1	0.391	-0.391		0.760	-0.760		0.627	-0.627		0.716	-0.716		0.858	-0.858
$A$9.0-s3p2	0.422	-0.422		0.628	-0.628		0.698	-0.698		0.595	-0.595		0.865	-0.865
$A$9.0-s3p3d2	0.421	-0.421		0.876	-0.876		0.697	-0.697		0.158	-0.158		0.853	-0.853
$A$9.0-s3p3d2f2	0.421	-0.421		0.877	-0.877		0.697	-0.697		-0.062	0.062		0.850	-0.850

Both the systems are known to be notorious cases because of the difficulty in calculating the effective charges [20]. We see that the effective charges by the CWFs quickly converge as a function of basis functions, while those by the Mulliken population are highly dependent on the choice of the basis function [48]. The non-ionic nature of the CN bond in the HCN molecule, obtained by the CWF method, is consistent with the picture given by the intrinsic atomic orbital method (IAO) [20]. On the other hand, it turns out that the effective charges calculated by MLWFs are relatively sensitive to the choice of basis functions compared to the cases of CWF, and exhibit large charge transfer in HCN and NaCl. The resultant ionic CN bond in the MLWF method differs from the picture derived by the IAO and CWF methods. The overestimation of the charge transfer in the MLWF method can be understood by comparing the WFs as shown in Fig. 7. It is confirmed that the CWFs (a)-(i) well preserve the shape of the atomic orbitals as expected. By contrast, the MLWFs (j), (k), (l), (o), and (p) deform significantly from the shape of atomic orbitals as a result of the maximally localization of the spread function. The MLWFs (j) and (k), originating from H-$1s$ and C-$2s$ orbitals, respectively, reduces the occupations by the deformation, while the occupations of the MLWFs (l), (o), and (p) increase due to the deformation. The $\sigma$ bonds between H-C and C-N are contributed by the MLWFs (l) and (p), respectively, which originate from C-2$p_x$ and N-2$p_x$ orbitals, respectively. Thus, the MLWF (j), originating from H-$1s$ orbital, does not largely contribute to the $\sigma$ bonds between H-C, reducing the population on the H atom. Similarly, the population on the N atom increases, since the $\sigma$ bond between C-N is formed by the MLWF (p), originating from N-$2p_x$. It is apparent that attributing the occupation of the MLWFs (l) and (p) to a single atom is not justified due to the fact that they are bond-centered. This implies that MLWFs should not be used to decompose electron population to each atom as demonstrated for the HCN molecule. On the other hand, CWFs are closest to atomic orbitals when the atomic orbitals are used as the guiding functions, and the population calculated by the CWFs can be naturally attributed to each atom, which allows us to calculate the atomic populations in a physically convincing manner.

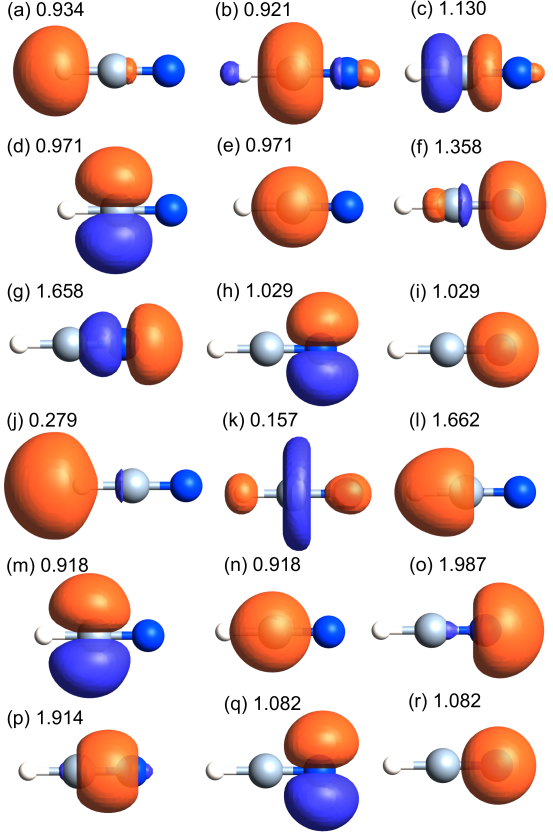
Figure 7: Wannier functions of a HCN molecule calculated by (a)-(i) the CWF and (j)-(r) the MLWF methods. The number that follows is the occupation number considering the degree of spin degeneracy. The white, silver, and blue spheres correspond to hydrogen, carbon, and nitrogen atoms, respectively. In all the cases, isovalues of $\pm 0.08$ (orange:0.08, blue:-0.08) are used for drawing the isosurfaces using OpenMX Viewer [40]. The computational conditions are the same as for the cases of A6.0-s3p3d2f2 in Table III.

For comparison, we also calculated the effective charges using the projection-only Wannier functions (POWF) [8] and found that the obtained values are relatively sensitive to the choice of basis functions and lie between the results obtained by the CWF and MLWF methods. Here, we analyze why the results from the POWF deviate from those by the CWF even when the inner window scheme [8] was used to focus on the valence states. In the HCN molecule, the projection of the $s$-orbital for hydrogen and the $s$-, $p_x$-, $p_y$-, $p_z$-orbitals for carbon and nitrogen results in nine Wannier functions. Since there are five occupied orbitals, applying the inner window scheme to the energy range of these orbitals first selects a subspace spanned by them. Subsequently, four vectors are chosen from the subspace consisting of unoccupied orbitals so that they can be orthogonal to the former subspace and have maximal overlap with the subspace obtained by projection of guiding functions onto a subspace spanned by states included in the outer window. Once the latter subspace is selected, each subspace is given equal weight in constructing the projection matrix. As a result, the nine Wannier functions generated are not specifically designed to primarily accommodate the occupied orbitals. This statement can be verified using the CWF method: By setting the window function with ${\epsilon }_0=-22.0$ eV, ${\epsilon }_1=8.0$ eV, and $k_{\mathrm{B}}{T}_0=k_{\mathrm{B}}{T}_1=0.1$ eV in the CWF method, and calculating the effective charges, contributions from low-lying unoccupied orbitals are included equally. We confirmed that this calculation results in effective charges nearly equivalent to those obtained by the projection-only method (not shown). It is evident that even when using the inner window scheme with the projection-only approach, properly computing effective charges remains a challenge. To calculate the effective charges assigned to atoms, it is reasonable to use atomic orbitals as projection orbitals. Typically, the number of atomic orbitals used exceeds the number of occupied orbitals, leading to similar challenges as observed in the case of NaCl. A simple solution to resolve this problem is to introduce a smoothly varying window function even in the inner window scheme when constructing the projection matrix. In fact, we confirmed that introducing a smoothly varying window function in the inner window scheme almost reproduces those by the CWF method (not shown). However, one should note that the use of the smoothly varying window function in the CWF is a much simpler method.

The Bader analysis shows erratic charge transfer in the CN bond, implying the limited applicability of the Bader analysis based on a real-space decomposition to the triple bond [20], while the effective atomic charges in NaCl are similar to those by the MLWF method.

It is considered from the comparison that the effective atomic charges obtained from the CWFs could serve as a valuable tool for analyzing electronic structures in a manner related to the approach discussed in Ref. [20]. Further investigation in this direction will be conducted in future studies.

V CONCLUSIONS

We presented a non-iterative method to calculate the closest Wannier functions (CWFs) to a given set of localized guiding functions such as atomic orbitals, hybrid atomic orbitals, and molecular orbitals (MOs). We defined the distance measure (DM) function $F$ by the sum of the squared distance between the projection functions $L$ and Wannier functions $W$ in the Hilbert space, and considered minimizing the DM function. It was shown that the minimization of the DM function is achieved by the polar decomposition of the projection matrix $A$ with a window function via the singular value decomposition (SVD) in a non-iterative manner. The CWFs can be uniquely constructed as long as the projection matrix $A$ is positive definite. It was also shown that the method is free from subtle choice of the gauge. The disentanglement of bands is naturally taken into account by introducing a smoothly varying window function, and including $N_{\mathrm{band}}$ Bloch functions to generate $N_{\mathrm{CWF}}$ CWFs, where $N_{\mathrm{CWF}}\le N_{\mathrm{band}}$. Even for isolated bands, the method always performs the disentanglement of bands without any iterative calculation and difficulty. The advantage of the smoothly varying window function over the inner window scheme [8] was clearly demonstrated in the disentanglement of $d$-bands in copper and in the calculations of the effective charges. Also, it is noted that the implementation of the method is relatively simple, which requires mainly matrix-matrix product and SVD. We have implemented the proposed method into the OpenMX code, which is based on the density functional theory (DFT), numerical pseudo-atomic orbitals (PAOs), and norm-conserving pseudopotentials (PPs), and introduced three types of guiding functions, i.e., atomic orbitals, hybrid atomic orbitals, and embedded MOs in molecules and bulks. The first two are easily employed from the PAOs. For the last one, we developed a method to calculate embedded MOs in molecules and bulks, which focuses on a partial trace formula of the projection operator for the occupied space and applies SVD to the partial matrix for the projection operator. The interpolated bands by tight-binding (TB) models derived from the CWFs reproduce well the targeted conventional bands of a wide variety of systems including Si, Cu, the TTF-TCNQ molecular crystal, and a topological insulator of Bi${}_2$Se${}_3$. These successful reproduction of targeted bands clearly demonstrates a wide variety of applicability of the proposed method. We further show the usefulness of the proposed method in calculating effective atomic charges, implying that the CWFs closest to atomic orbitals can be used as a measure to analyze electronic structures from one system to the others. Thus, we conclude that the proposed method is an alternative way in efficiently calculating WFs, and the concept of CWFs will provide a basis for development of novel methods of analyzing electronic structures and calculating physical properties [49, 50].

Appendix A: The upper bound of the diagonal elements of the matrix $D$

A proof for the upper bound of the diagonal elements of the matrix $D$ is given in the appendix. Note that $UV$ and $BV$ in Eq. (11) are partial unitary matrices in size of $N_{\mathrm{band}}\times N_{\mathrm{CWF}}$. Since $D$ is hermitian, its eigenvalues are real. Let $\lambda$ be an eigenvalue of $D$ and $x$ be the corresponding eigenvector. Then, the following equation holds:

${\displaystyle \frac{1}{2}}\left(V^{†}{U}^{†}BV+V^{†}{B}^{†}UV\right)|x⟩=\lambda |x⟩.$ (35)

Defining $|y⟩=UV|x⟩$ and $|z⟩=BV|x⟩$, and operating $⟨x|$ from the left side of Eq. (35), we have

$⟨y|z⟩+⟨z|y⟩=2\lambda ⟨x|x⟩.$ (36)

Noting $⟨y|z⟩+⟨z|y⟩\le 2|⟨y|z⟩|$, and using the Cauchy-Schwarz inequality $|⟨y|z⟩|\le \sqrt{⟨y|y⟩⟨z|z⟩}$, we obtain

$⟨y|z⟩+⟨z|y⟩\le 2\sqrt{⟨y|y⟩⟨z|z⟩}.$ (37)

Since $⟨y|y⟩=⟨z|z⟩=⟨x|x⟩$, combining Eq. (36) and Eq. (37) results in

$\lambda ⟨x|x⟩\le ⟨x|x⟩.$ (38)

Considering $⟨x|x⟩\ne 0$, the upper bound of the eigenvalues of $D$ is found to be

$\lambda \le 1.$ (39)

Noting that the matrix $D$ can be written by $x$ and $\lambda$ as

$D={\displaystyle \sum _{\nu }}|x_{\nu }⟩{\lambda }_{\nu }⟨x_{\nu }|,$ (40)

the diagonal elements $d_{nn}$ of the matrix $D$ is given by

$d_{nn}={\displaystyle \sum _{\nu }}{|⟨n|x_{\nu }⟩|}^2{\lambda }_{\nu },$ (41)

where $⟨n|x_{\nu }⟩$ is the $n$-th element in the vector $x_{\nu }$. Since the upper bound of $\lambda$ is unity, and $\{x\}$ forms a unitary matrix, we obtain the upper bound of the diagonal elements of the matrix $D$ as

$d_{nn}\le 1.$ (42)