O() Krylov Subspace Method: Ver. 1.1
The original has been published
in Phys. Rev. B 74, 245101 (2006).
Abstract
An efficient and robust O() method is presented for fully self consistent large scale ab initio electronic structure calculations. A detailed short range and an effective long range contributions to the electronic structure are taken into account by solving an embedded cluster defined in a Krylov subspace, which provides rapid convergent results for not only insulators but also metals. As illustrations of capability of the method, we present three large scale calculations based on density functional theory: (i) calculation of full wave function of DNA, (ii) interaction between a carbon nanotube and metal surface, and (iii) geometry optimization of boron doped diamond, which clearly show that the method is a promising approach for realization of large scale ab initio calculations for a wide variety of materials including metals.
1 INTRODUCTION
The development of O() or linear scaling method is a promising direction of extending applicability of ab initio electronic structure calculations based on density functional theory (DFT) to large scale realistic systems.[1, 2, 3] In fact, over the last decade, considerable efforts have been devoted to establish efficient and robust O() methods [2, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 20], and successful applications within non-self consistent field (SCF) tight binding (TB) scheme [24, 25, 26] and a number of benchmark calculations within the fully SCF DFT have been reported.[9, 10, 11, 27, 28, 29] Nevertheless, within the fully SCF DFT much improvement is still needed to reduce the error below chemical accuracy (a few milli-Hartree/atom at least), referred to as milli-Hartree accuracy hereafter, for a wide variety of materials with modest computational cost. In addition, the application to ab initio calculations tends to be practically hampered by an intractable feature that an approximate solution of eigenstates by the O() methods often induces instabilities in the SCF calculation. In this paper to overcome these difficulties we present an efficient and robust O() method for a wide variety of materials including metals in which ideas behind two O() methods, divide-conquer (DC) [4] and recursion methods,[14, 15, 23] are unified in a single framework.
The principles behind the O() methods which have been proposed so far can be roughly classified into two categories: variational principles [6, 7, 8, 9] and perturbative principles,[4, 5, 12, 13, 14, 16, 17, 18, 19], while the other O() or O() methods that cannot be simply classified into these categories exist.[20, 21, 22] Three O() methods we discuss in this paper belong to the latter. In the former the local quantity of wave functions or density matrix in real space is explicitly affected by all the elements of the Hamiltonian for the whole system. On the other hand, in the latter it is determined by a finite range interaction with an implicit coupling with the whole system via the Poisson equation. This feature may be related to numerical robustness of both the classified methods, which has been not well understood yet. Meanwhile, it is known that the DC method provides rapid convergence for covalent systems such as biological molecules with numerical stability during the SCF calculation.[4] However, the application of the DC method to metals is significantly restricted by requirement of the large size of truncated cluster. On the other hand, the recursion method based on Lanczos algorithms and the Green functions is one of suitable methods for metals,[5, 14, 15, 23] although the SCF calculation with the recursion method becomes unstable. The main idea behind the recursion method is to employ a Krylov subspace [16, 17, 30] generated by the Lanczos algorithm in evaluating the Green functions.[23] The dimension of the Krylov subspace, required for the convergence with respect to the total energy in metals by the recursion method, is generally much smaller than that of the original vector space defined by the truncated cluster,[14] which is the reason why the recursion method can be efficient for metals. Thus, we propose a novel method which possesses the advantages in two methods and overcomes the drawbacks. This paper is organized as follows: In Sec. 2 the theory of the proposed method is presented with comparison among three O() methods and with technical details for the practical implementation. In Sec. 3 the convergence properties of the total energy and selected physical quantities are presented for insulators, semiconductors, metals, and molecular systems. In Sec. 4 three applications of the method are discussed to illustrate aspects in practical applications. In Sec. 5 we summarize the theory, applicability, and limitation of the O() method.
2 THEORY
2.1 General
Let us assume that the basis set consists of nonorthogonal localized functions such as pseudo-atomic orbitals (PAO) [31] and finite elements basis.[32] Throughout this paper we use the PAO as basis function to expand one-particle wave functions.[31] The charge density associated with spin component is evaluated via density matrix by
| (1) | |||||
where is a basis orbital, a site index, and an orbital index for the basis function. The final relation of Eq. (1) represents a basis for three O() methods that the charge density is given by the sum of the contributions from each site. Indeed the three O() methods we discuss are methods of calculating approximately the local charge density . The density matrix is calculated using the one-particle Green function by
| (2) |
where is the Fermi function, and is a positive infinitesimal. Since the imaginary part of the Green function gives the density matrix in an integrated form, the evaluation of the density matrix can be replaced by the evaluation of the Green function. The spin index will hereafter be dropped for simplicity of notation. It is noted that only the charge density and the density matrix are required in the conventional DFT. The contribution of kinetic term to the total energy is expressed as a function of the density matrix, and the other contributions are written as a functional of the charge density.[33] Therefore, it would be enough to discuss how the density matrix can be evaluated using the Green function in an O() computational effort, and we will focus on the evaluation of the Green functions in later discussion.
The proposed method can be regarded as a unified scheme which bridges the DC and recursion methods, therefore, before discussing the proposed method, let us summarize two linear scaling methods: the DC and recursion methods. Both the methods provide different ways of evaluating the Green functions from a local Hamiltonian and overlap matrices constructed from the local environment for each site .[4, 5, 14] For each site a truncated cluster is constructed by taking account of the local arrangement of basis functions as depicted in Fig. 1(a), indicating that the truncated cluster can overlap largely each other and can contain the same sites as the neighboring sites. In this study we construct the truncated clusters by using both the physical and logical truncation schemes [15] which will be explained later. Basis functions belonging to the truncated cluster span a subspace in the total vector space spanned by a set of basis functions in the whole system, i.e., .
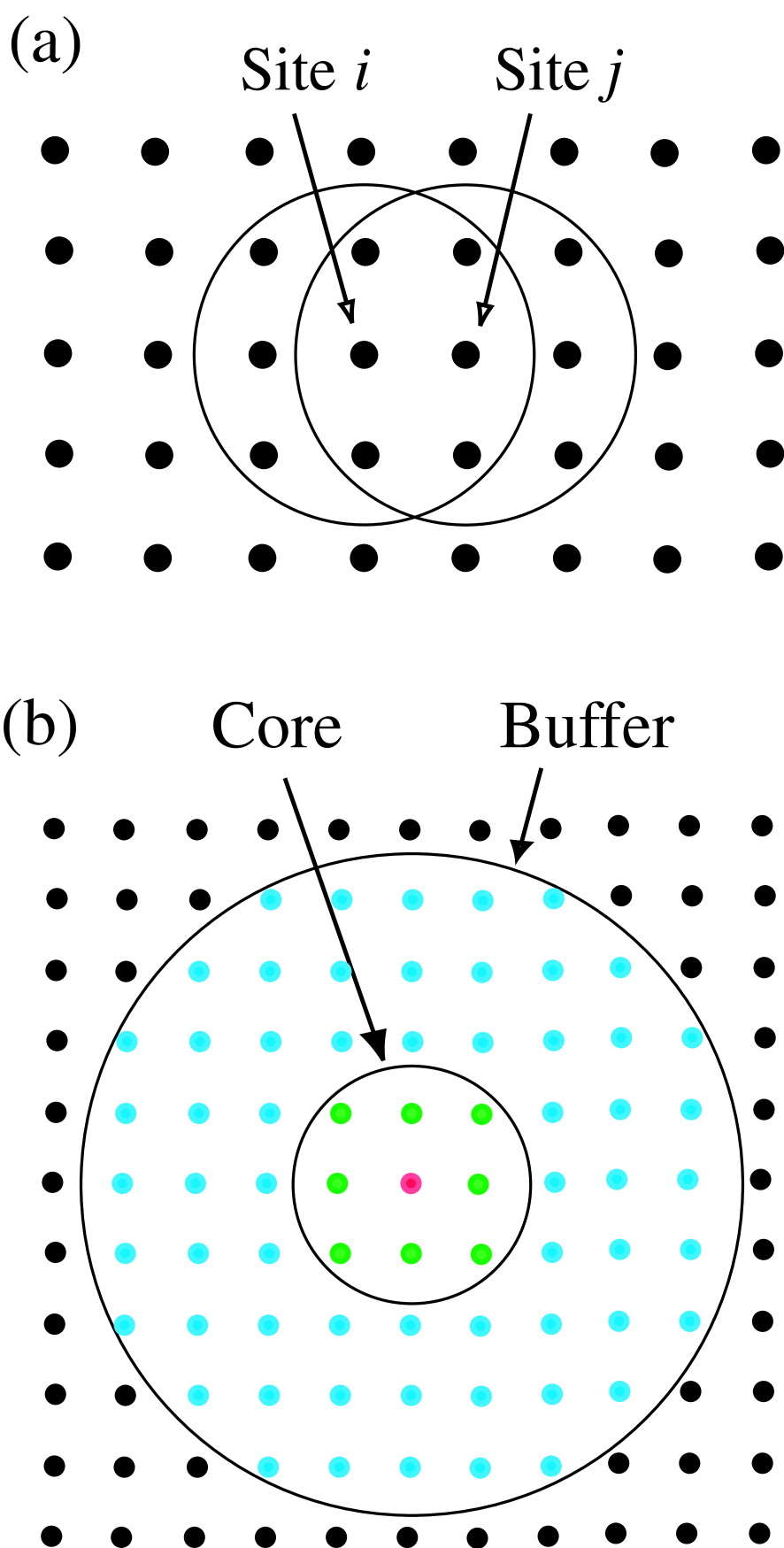
Figure 1: (Color online) (a) Schematic view of truncated cluster centered on sites i and j. (b) Schematic view of spatial division of a truncated cluster into a core (green) and the remaining buffer (blue) regions. The circles represent the center of localized basis functions in real space.
For each truncated cluster , a local Hamiltonian and overlap matrices are constructed for the DC and recursion methods in the completely same way. The simplest way of finding an approximate Green function from the and is to diagonalize directly the corresponding eigenvalue problem:[35]
| (3) |
Using the eigenvalues and eigenstates of Eq. (3), the local Green function is simply given by
| (4) |
where is a complex number, and is dropped for simplicity of notation, and we will drop it for later discussion unless unambiguity is lost. The evaluation of the Green function by the direct diagonalization is the DC method proposed by Yang.[4] The elements in the density matrix associated with the site can be found through Eq. (2) from the local Green function Eq. (4). It is important to notice that in the evaluation of the Green function only diagonal and off-diagonal elements associated with the central site are calculated from the eigenvalue problem Eq. (3) for the site , and that all the elements of the Green function required in the calculation of Eq. (1) are constructed as the sum of parts of the Green function. For a generalization of the central site see the AppendixA. This patch work of the Green function is the common strategy of the three O() methods we discuss, and is based on a physical intuition that the local electronic structure of each site can be approximately determined from the local atomic arrangement. We will justify this patch work by discussing a relation between the local Green function and moments of local density of states later on.
On the other hand, the recursion method [5, 14, 15, 23] adopts a different way of evaluating the Green function in which the original vector space defined by basis functions in the truncated cluster is mapped to a Krylov subspace with a smaller dimension rather than solving directly the eigenvalue problem like the DC method. In the recursion method [14] generalized to non-orthogonal basis, the Krylov subspace generated by a two-sided Lanczos algorithm is given by
| (5) |
where , the number of recursion levels in the Lanczos transformation, and with basis orbitals on the site having basis functions. In later discussion we will not distinguish a notation representing the subspace and that for a set of vectors spanning the subspace. By making full use of a result that the Hamiltonian matrix is transformed by the Lanczos algorithm into the block tridiagonal matrix, the elements of the Green functions associated with the central site can be evaluated by using a multiple inverse and a recurrence relation instead of diagonalizing the matrix.[14] In general the dimension of needed for the convergence is much smaller than that of , which implies . Thus, the computational effort can be significantly reduced compared to the DC method. Although the recursion method provides convergent results for a wide variety of materials in a smaller dimension of within non-SCF TB schemes,[5, 14, 15, 23] we will show in Sec. 3 that the recursion method tends to suffer from the numerical instability when the method is combined with SCF calculations.
2.2 Unified method
As discussed above, although the DC method is a simple and robust scheme, the direct diagonalization in this scheme is often impractical for metallic systems, where the size of truncated cluster could be large to achieve the milli-Hartree accuracy. In contrast, the computational effort in the recursion method can be reduced by mapping the original vector space defined by the truncated cluster to a smaller subspace, while the numerical instability during the SCF calculation is a serious problem. Thus, to overcome the drawbacks we propose a unified method which bridges the DC and recursion methods. It is worth mentioning that recently a similar idea has been independently proposed by Takayama et al. within a non-SCF orthogonal TB model.[16, 17] To see why the recursion method can provide convergent results by a smaller Krylov subspace , taking account of for , the Green function given by Eq. (4) can be rewritten as
| (6) |
with a moment in a matrix form defined by
| (7) | |||||
where is a matrix of which column vectors consist of the eigenvectors, and a diagonal matrix consisting of the eigenvalues. To obtain the final equation of Eq. (7), note that . The moment representation of the Green function by Eq. (6) clearly shows that the Green function can be approximated by terminating the summation for the moments at a finite order. Meanwhile, it is easily shown using Eq. (7) that the Hamiltonian represented by the Krylov subspace Eq. (5) can be expressed by up to ()th moments:
| (8) | |||||
where the underline of means a block element of the matrix. Since the indices and run from 0 to , one can see that the Hamiltonian for represented by the Krylov subspace is constructed by up to ()th moments. This relation represents that the Green function evaluated from contains up to ()th moments in the summation of Eq. (6).[36] The lower order moments play an important role on description of the Green function,[5] and the contribution decreases significantly as the order increases. Considering that the contributions are included from the moments of the lower order in the recursion method based on a Krylov subspace, we see that the fact assures the rapid convergence in the recursion method, while it is difficult to incorporate it into the SCF calculation due to the numerical instability.
Therefore, by taking account of the rapid convergence in the recursion method and the robustness of the DC method with respect to numerical stability, we now develop a DC method defined in a Krylov subspace. Considering that the Krylov subspace [30, 16] can be generally defined by Eq. (5) for the non-orthogonal basis set, first let us introduce a Krylov subspace for each site given by
| (9) |
where , and are eigenvalues and corresponding eigenvectors of an overlap matrix . The subspace W is generated by the following algorithm:
| (10) |
| (11) |
| (12) |
| (13) |
| (14) |
| (15) |
| (16) |
where the operator means that the overlap integral between basis functions is taken into account in the calculation of the norm between vectors, and the orthogonality among vectors under the consideration is called -orthogonality, while that defined by the conventional norm of vectors is called -orthogonality throughout this paper. In the generation of a Krylov subspace given by Eqs. (10)-(16), we impose only the -orthogonality between Krylov vectors without assuming any specific form for the representation of the Hamiltonian matrix, while a tridiagonal form of the Hamiltonian matrix is imposed in the Lanczos algorithm.[5, 14, 23] In principle, although the procedure by Eqs. (10)-(16) gives a set of -orthonormal Krylov vectors because of the introduction of the Gram-Schmidt orthogonalization by Eq. (12), however, the -orthonormality is not well assured due to round-off error in the Gram-Schmidt process. Therefore, the Krylov subspace is given by an orthogonal transformation Eq. (9) which keeps the transformed vectors spanning the same Krylov subspace. One may think that the Gram-Schmidt orthogonalization Eq. (12) is now unnecessary because the Krylov vectors are finally orthogonalized by the transformation Eq. (9). However, if we skip the Gram-Schmidt orthogonalization in the algorithm, a set of generated vectors by Eq. (11) tends to be linearly dependent on the Kryrov vectors generated at the previous steps in the middle of the procedure by Eqs. (10)-(16). Thus, it would be important to include the Gram-Schmidt orthogonalization for the numerical stability.
In this algorithm Eqs. (10)-(16), might be the inverse of a local overlap matrix constructed from the same truncated cluster as in the construction of the local Hamiltonian , where the cluster is constructed by the logical truncation method as discussed above. In case the large size of truncated cluster is required to achieve the milli-Hartree accuracy, it can be a hard task to calculate the inverse of . Thus, can be substituted by an approximate inverse. Although a lot of efficient methods of inverting the overlap matrix have been proposed so far, we now propose a method of calculating an approximate inverse based on a Krylov subspace of which idea is very similar to that considered in Ref. [34]. In the method an approximate inverse can be evaluated by
| (17) |
where , and generated by the following algorithm:
| (18) |
| (19) |
| (20) |
| (21) |
| (22) |
| (23) |
| (24) |
The algorithm Eqs. (18)-(24) generates a Krylov subspace given by
| (25) |
The introduction of the Gram-Schmidt orthogonalization Eq. (20) is due to the same reason as in the generation of the Krylov subspace . Noting that , , and , we can easily obtain Eq. (17) as an approximate inverse. As well in Eq. (8), the overlap matrix represented by the Krylov subspace Eq. (25) can be related to the moment as follows:
| (26) | |||||
where is a moment defined by eigenvalues and eigenvectors of the local overlap matrix for the truncated cluster. Since and run from 0 to , the overlap matrix associated with is constructed by up to ()th moments, indicating that contains ()th moments. Besides the method based on a Krylov subspace, we also implemented two other methods of calculating the inverse approximately: an incomplete Cholesky decomposition and a Neumann series expansion [37] with second, third, or a higher order expansion. However, it turned out that the Krylov subspace method is more efficient than the two methods.
We have not discussed yet how we should choose the initial sets of states and used in these algorithms for generation of Krylov subspaces. In this study the initial sets of states and consist of block I-orthonormalized vectors and its -orthonormalized vectors. However, it should be noted that the optimum choice of depends on the system under consideration. A possible way of choosing is to use a set of basis functions on the central site , which is similar to that in the block bond order potential method.[14, 15] Another choice is to use a set of basis functions on the central site plus the neighboring sites. In most of calculations in this study we use the latter choice for the numerical robustness, since the former tends not to conserve the symmetry of charge distribution to be expected in symmetric systems due to round-off error. The round-off error in the generation of Krylov subspace is accumulated as the iteration step in the procedure by Eqs. (10)-(16) increases, and the accumulation tends not to be negligible by the increase of the number of iteration steps in case of a smaller dimension of . In this study for the latter case the initial state is constructed by basis functions belonging to atoms within a sphere with a radius of , where is the distance between the central atom and the nearest atom.
For numerical stability, it is crucial to construct the Krylov subspace at the first SCF step, and to fix it during subsequent steps. If the Krylov subspace is regenerated at every SCF step, the SCF convergence becomes significantly worse because of fluctuation of the spanned space, which is the reason for the instability inherent in the recursion method coupled with the SCF calculation. If the dimension of is smaller than that of , the generated Krylov subspace depends on the Hamiltonian through its multiplication given by Eq. (11). The fluctuation of the spanned space may couple with the self consistent process of charge density in an indeterminate way as shown in the Sec. 3.
We are now ready to make full use of the Krylov subspace generated by above procedures. By using the Krylov subspace vectors generated by the algorithm Eqs. (10)-(16), one can transform the representation of Hamiltonian from the original basis set into the Krylov vectors. In the transformation of the representation, we furthermore consider a spatial division of the truncated cluster into a core and the remaining buffer regions as shown in Fig. 1(b). The core region in this study is defined by a cluster which is constructed by sites having non zero overlap to the central site . Then, the original generalized eigenvalue problem for the truncated cluster can be transformed to a standard eigenvalue problem
| (27) |
with
| (28) | |||||
where , , and are Hamiltonian matrices, represented by the original basis functions , for the core and buffer regions, and between the core and buffer regions, respectively. Because of the orthogonal transformation Eq. (9), it is assured to be , and one can obtain the standard eigenvalue problem instead of a generalized problem. Considering that the Krylov subspace is decomposed to two contributions consisting of the core and buffer regions: , it is straightforward to see that is composed by a short range and the other long range contributions . Since the required buffer size to satisfy the milli-Hartree accuracy can be large in most cases for metals, therefore, once the long range contributions is calculated at the first SCF step, the matrix can be fixed during subsequent steps, while it it possible to update after achieving the self consistency or to recalculate at every SCF step. Then, the standard eigenvalue problem is diagonalized with an updated and the fixed during subsequent steps, which means that the detailed short range contribution to the electronic structure can be taken into account with an effective correction by the long range contribution . As a result, the evaluation of the Green functions is mapped to a cluster problem analogous to the DC method [4] but with the effective smaller Hamiltonian , which is the meaning of what we intend by the DC method defined in the Krylov subspace. Noting that in the density matrix elements having non zero overlap to the central site can contribute to the charge density Eq. (1), the components in the eigenvectors required to calculate corresponding density matrix elements is easily evaluated by a back transformation . It is also noted that the evaluation of the Green function and the density matrix Eq. (2) is trivial in the same way as for Eq. (4) in the DC method,[4] since we have the eigenvalues and its corresponding eigenvectors .
The Green functions are constructed from the eigenvalue and its corresponding eigenvectors as discussed above, therefore, it is apparent that the method cannot give a finite DOS at the Fermi energy properly for metallic systems, since the resultant density of states (DOS) is discrete. However, in the evaluation of the density matrix, and can be regarded as abscissa and weight in a quadrature,[38] while to my knowledge the statement has not been proven rigorously within the non-orthogonal basis set. Thus, it is expected that the density matrix being an integrated quantity can be accurately evaluated unless we focus attention on details of the density of states. For a proper calculation of the DOS an alternative scheme will be discussed in the Sec. 4.
2.3 Details on implementation
In this subsection technical details on the implementation of the proposed method are given in an algorithm fashion in order to comprehend the computational flow. The SCF calculation can be performed by a sequence (1)-(2)-(3)-(4)-(5)-(2)-(4)-(5)-(2)-(4)-(5)-… in terms of the following procedures:
(1) Truncation of system:
A large system is divided into small truncated clusters by the physical and logical truncation schemes.[15] After picking neighboring sites up within a sphere with a radius of , which is the physical truncation, we furthermore reconstruct a truncated cluster defined by all neighbors that can be reached by hops in the cluster consisting of the chosen sites, where the hopping is made when the distance between sites is smaller than the sum of cutoff radii of two localized basis functions which are placed in each site, respectively. The second scheme is called the logical truncation, and effective to reduce the energy jump in MD simulations, since isolated sites having no overlap with the other sites can be excluded in the truncated cluster. As a result, the truncated clusters can overlap largely each other as shown in Fig. 1(a).
(2) Construction of cluster Hamiltonian:
For each truncated cluster made by the procedure (1) the Hamiltonian and overlap matrices are constructed by the same way as in the conventional DFT calculation. It is worth mentioning that the Hartree potential is calculated by considering not only the charge density from the truncated cluster, but also all the contributions of truncated clusters in the whole system, which means that each truncated cluster is not isolated in vacuum, but embedded in the system without neglecting the long range Coulomb interaction. This treatment by the embedded cluster would be crucial for computational accuracy. The matrix elements associated with site can be calculated in a parallel computation without any communication, and communications among processors are performed to construct the cluster Hamiltonian and overlap matrices for each truncated cluster.
(3) Generation of Krylov subspace:
At only the first SCF step, the initial state is given by a set of basis functions on the central site of each truncated cluster or a set of basis functions on the central site plus the neighboring sites, the initial state is the -orthogonalized vectors of . After generating the Krylov subspace using Eqs. (18)-(24), is generated using Eqs. (10)-(16), where it is recommended for numerical efficiency to perform the multiplication associated with and in a matrix by vector fashion. Finally, the orthogonal transformation Eq. (9) yields the Krylov subspace with -orthogonal vectors. Then, we only have to store for subsequent steps. It is quite important to keep the subspace generated at the first SCF step for numerical robustness. The Krylov subspace for each truncated cluster is separately calculated on each processor without communication.
(4) Construction of effective Hamiltonian:
The short and long range contributions to the effective Hamiltonian are calculated by Eq. (28) on each processor without communication. When a large size of the buffer region shown in Fig. 1(b) is taken into account, the long range contribution calculated at the first SCF step can be used at subsequent steps for numerical efficiency.
(5) Self consistency
The standard eigenvalue problem with the effective Hamiltonian is diagonalized, and the back transformation yields a set of components of eigenvectors required for the calculation of charge density. Then, a common chemical potential for all the truncated clusters in the total system is found by a bisection method so that the total number of electrons in the total system can be conserved. To find efficiently the common chemical potential let us define a Green function in terms of Mulliken population by
| (29) | |||||
with
| (30) |
Using the Green function in terms of Mulliken population one can easily find the total number of electrons in the total system with a chemical potential as follows:
| (31) | |||||
where the factor 2 is for spin multiplicity. Thus, the common chemical potential to conserve the total number of electrons can be found by employing Eq. (31) and a bisection method in which the number of electrons in each truncated cluster are communicated among processors, and it is a very small amount of the communication. Once the common chemical potential is determined, the elements of the density matrix required for the calculation of the charge density Eq. (1) are evaluated by Eq. (2) with the common chemical potential. Because of the employment of the common chemical potential, note that electrons can flow from one truncated cluster to the other truncated clusters. After calculating the charge density of the whole system by Eq. (1) and mixing the charge density by an appropriate mixing scheme, the Hartree potential is calculated by solving the Poisson equation using a fast Fourier transformation (FFT) for not the truncated cluster but the whole system in which a lot of communications from all the processors to all the processors are required.
3 NUMERICAL RESULTS
3.1 Computational details
All the calculations in this study were performed by a DFT code, OpenMX,[33, 39] in which one-particle wave functions are expressed by the linear combination of pseudo-atomic basis functions (LCPAO) centered on atomic sites,[31] norm-conserving pseudopotentials are used in a separable form with multiple projectors to replace the deep core potential into a shallow potential,[40, 41] and a generalized gradient approximation (GGA) [42] to the exchange-correlation potential is used. The basis functions used are pseudo-atomic orbitals generated by a confinement scheme,[31] which are specified by H4.5-s2, B4.5-s2p1, C4.5-s2p1, N4.5-s2p1, O4.5-s2p1, Li8.0-s2, Al6.0-s2p2, Si6.0-s2p1d1, P6.0-s2p1d1, Fe4.5-s2p2d1, and Mn5.5-s2p2d1, where the abbreviation of basis functions, such as H5.0-s1p1, represents that H stands for the atomic symbol, 5.0 the cutoff radius (Bohr) in the generation by the confinement scheme, and s1p1 means the employment of one primitive orbital for each of and orbitals. The pseudopotentials used are found in Ref. [31]. The real space grid techniques are used with the energy cutoff of 180 Ry as a required cutoff energy in numerical integrations and the solution of Poisson equation using FFT,[43] while the cutoff energy is adjusted depending on the size of the unit cell so that the difference in the cutoff energies used for the a-, b-, and c-axes can be minimized. In addition, the projector expansion method is employed in the calculation of three-center integrals for the deep neutral atom potentials.[33] Electronic temperature of 300 K is used to count the number of electrons by the Fermi-Dirac distribution function for all the system we considered. In most cases for comparison the k-space conventional diagonalization is also performed with a large number of k-points so that the accuracy of Hartree/atom at least can be assured unless the number of k-points is explicitly specified.
3.2 Convergence properties
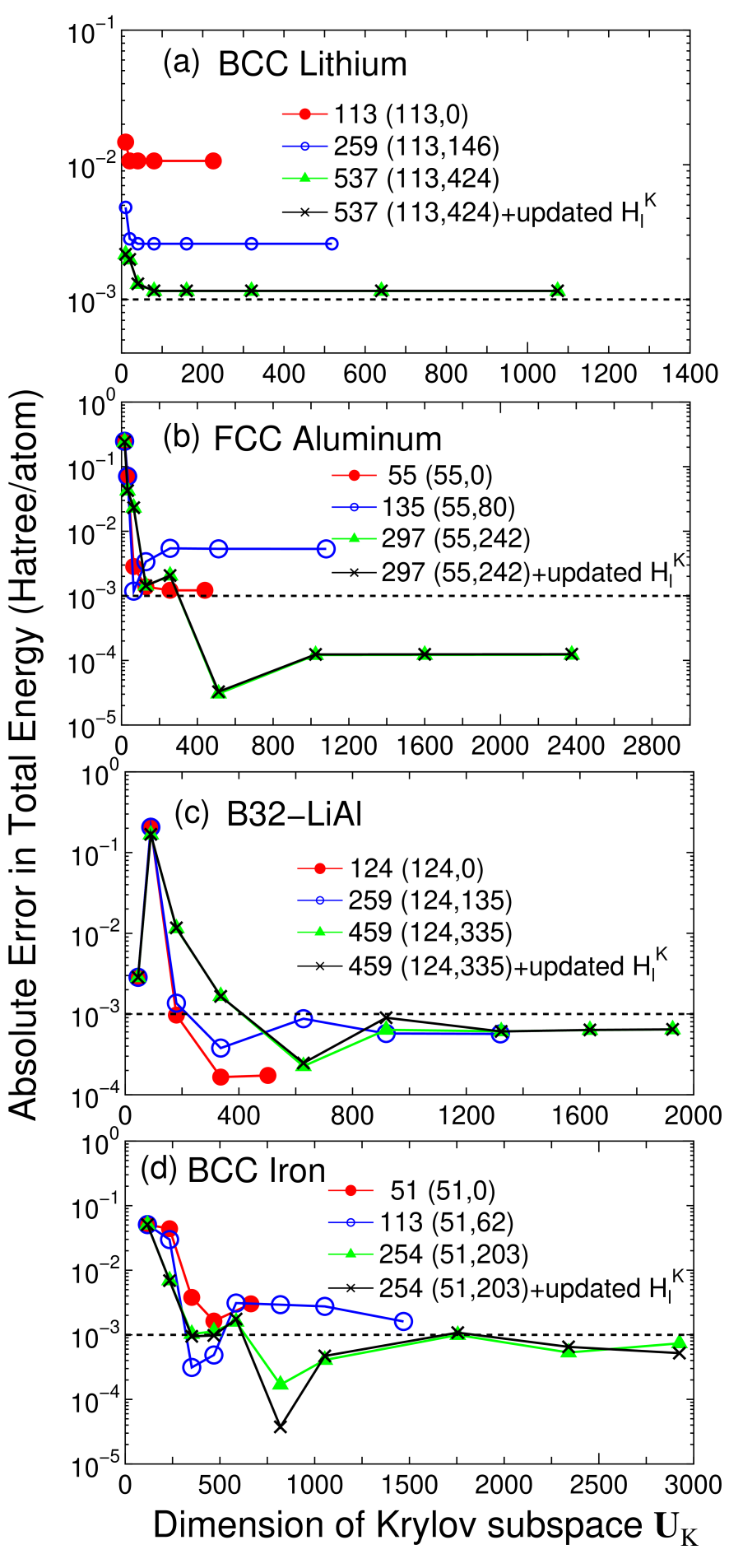
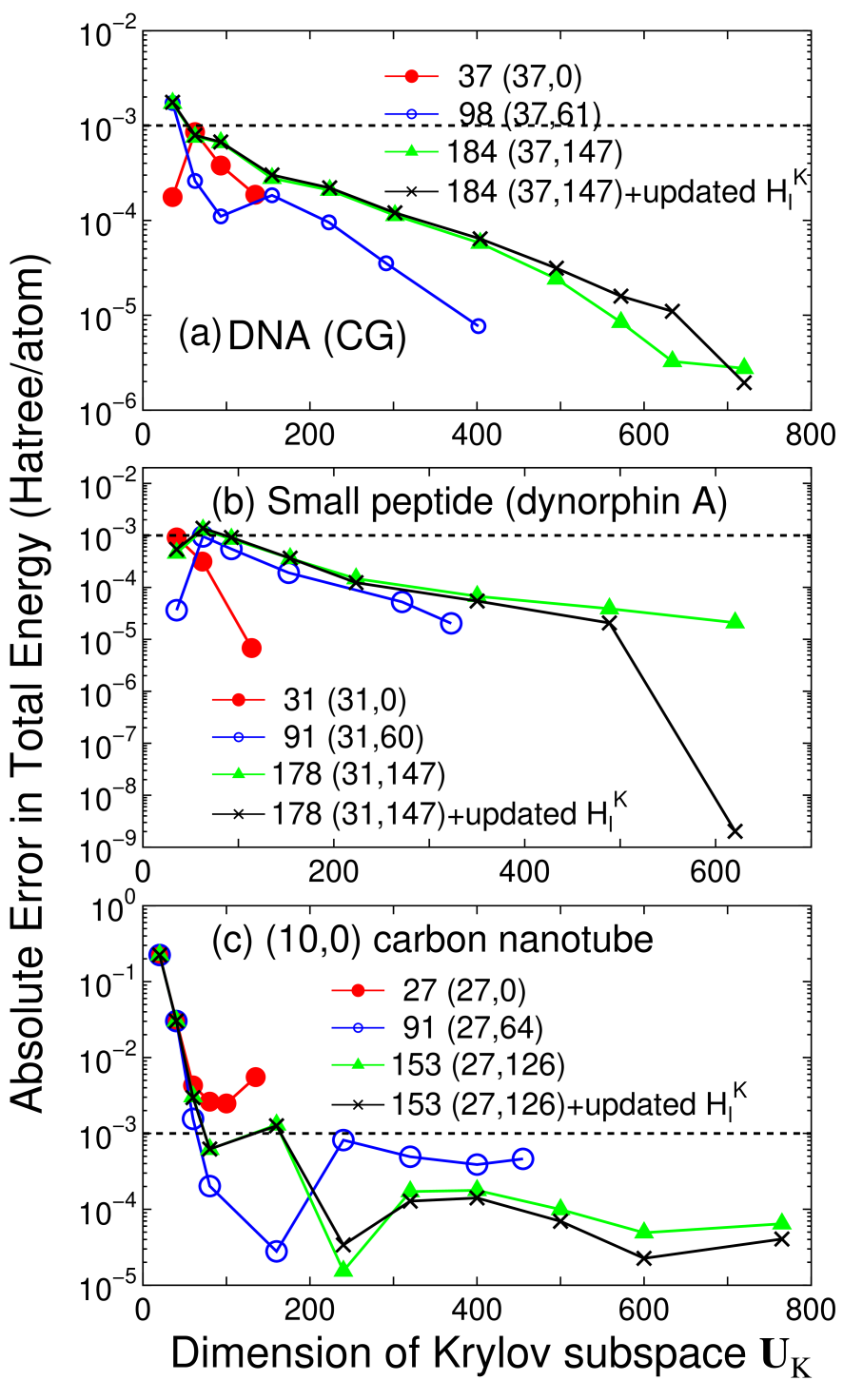
Accuracy and efficiency of the proposed method can be controlled by two parameters: the size of the truncated cluster and the dimension of the Krylov subspace , and an optimum choice of these parameters to achieve the milli-Hartree accuracy depends on systems under consideration. Thus, for a wide variety of materials convergence properties of the total energy are shown as a function of the two parameters in Figs. 2-4 for bulks with a finite gap, metallic systems, and low-dimensional molecular like systems, respectively. For geometrical structures we studied, the experimental coordinates are used for carbon and silicon in the diamond structure, manganese mono-oxide in the rock salt structure, BCC lithium, FCC aluminum, aluminum lithium alloy in the B32 structure, and BCC iron. For hexagonal ice the coordinates were generated by a geometry optimization with a CHARMM force field,[44] for deoxyribonucleic acid (DNA) and dynorphin A [45] the coordinates were generated using a software TINKER,[46] and for (10,0) carbon nanotube (CNT) the coordinates were generated with a bond length of 1.42 Å. The geometrical structures of the other systems will be given when they are discussed.
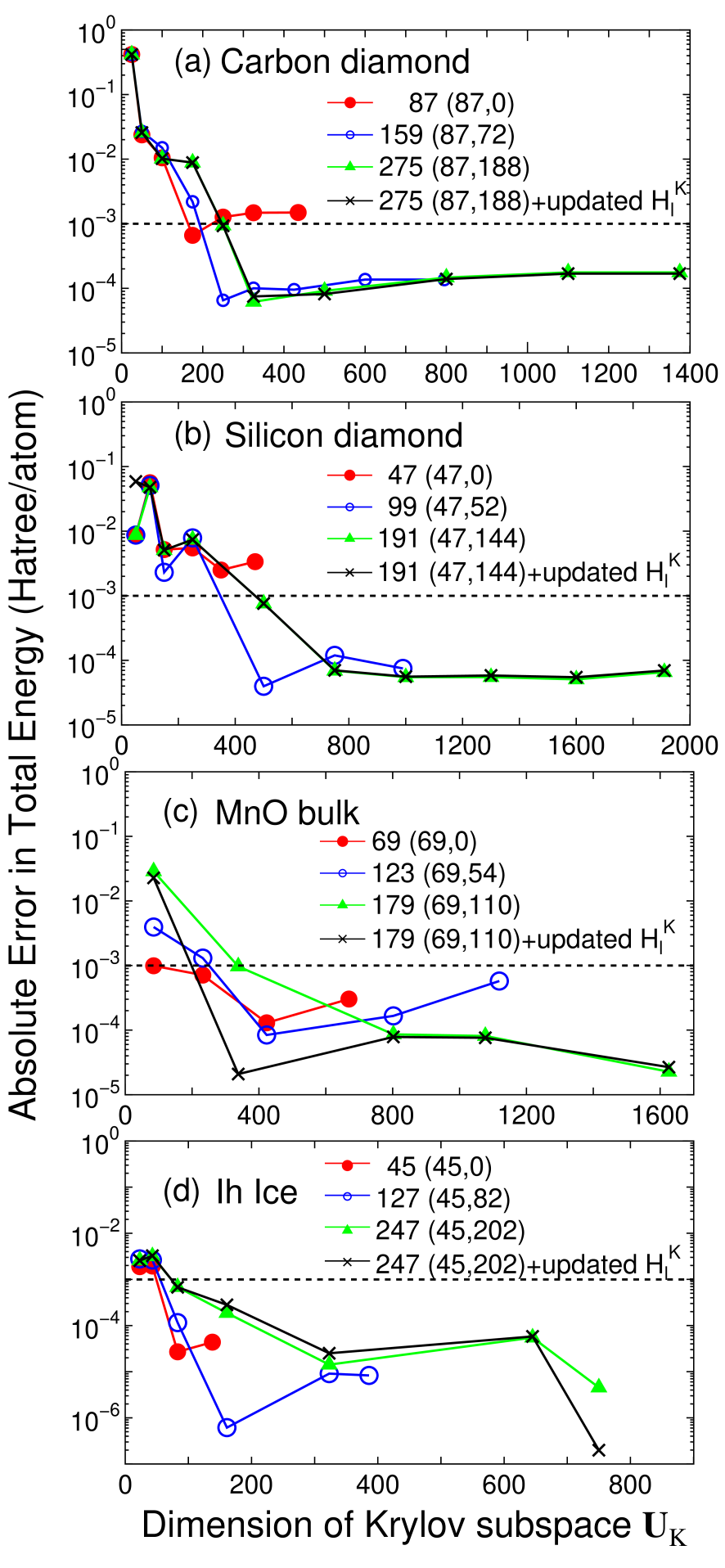
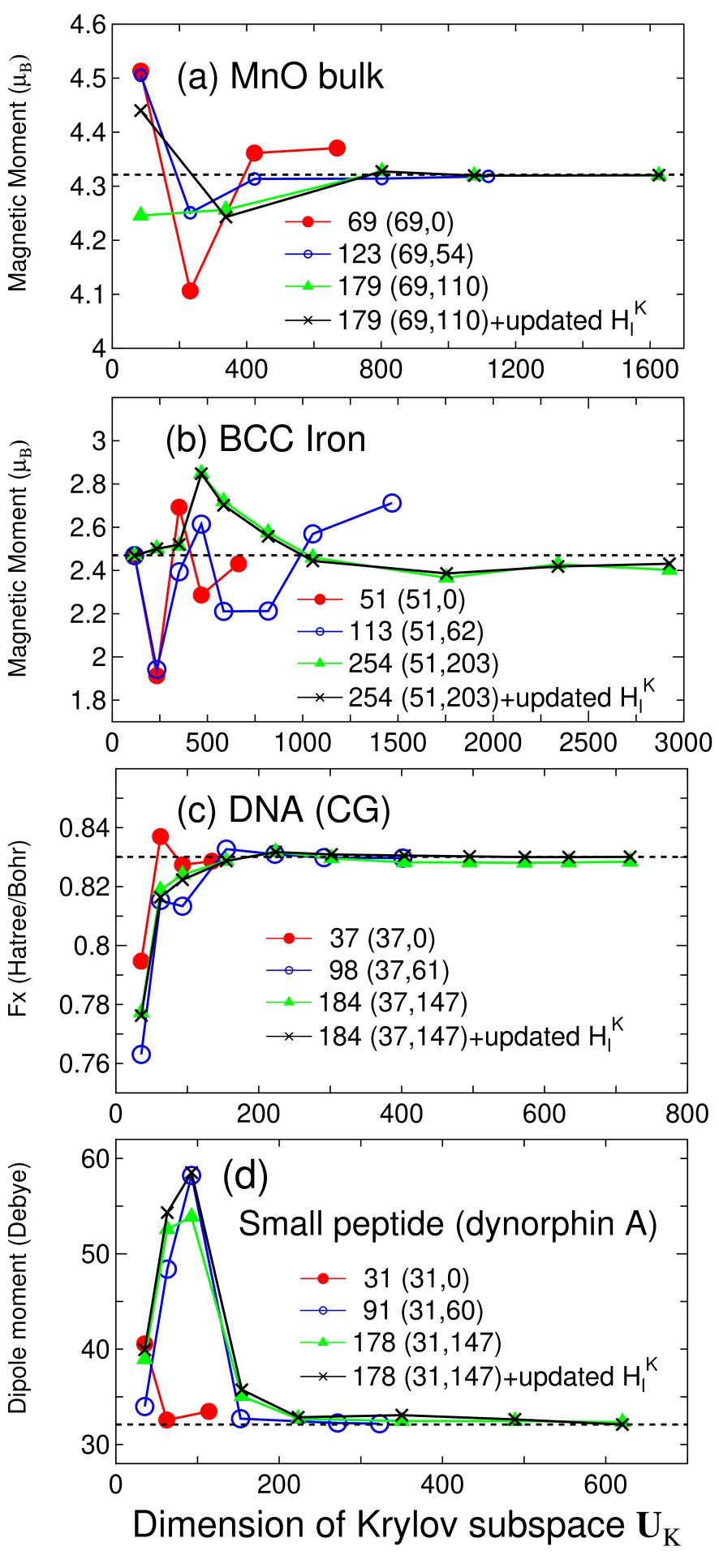
For bulks with a finite gap, we see that a truncated cluster consisting of 100-150 atoms reproduces the total energy calculated by the conventional k-space scheme within the milli-Hartree accuracy. For carbon and silicon in the diamond structure, the total energy converges rapidly as a function of the dimension of the Krylov subspace , and it suggests that about 40% of the total number of basis functions in the truncated cluster is enough for the convergence, where the largest dimension of the Krylov subspace for each size of truncated cluster in figures corresponds to the number of basis functions in the truncated cluster. In all the calculations by the proposed method, the dimension of Krylov subspace for the overlap matrix is taken as four times that of , since it turned out that an excess of approximation of leads a slow convergence of the total energy as a function of the dimension of the Krylov subspace . To see the error introduced by the fixed long range contribution a calculation using the updated is also shown, indicating that for carbon and silicon the absolute error by the fixed is less than Hartree/atom. Even for ionic bulk systems such as MnO bulk and ice, the absolute error in the total energy is less than Hartree/atom at about 40% of the total number of basis functions in the truncated cluster. On the other hand, the absolute error by the fixed is larger than that in the case of carbon and silicon. This is due to large variation in the charge distribution during the SCF process, which implies that for ionic systems it is better to update at every SCF step.
For simple metals such as BCC lithium and FCC aluminum, the total energy converges very rapidly as a function of the dimension of the Krylov subspace. However, a relatively large size of truncated cluster is required to achieve the milli-Hartree accuracy. Especially for BCC lithium, even the largest size of the truncated cluster consisting of 537 atoms does not satisfy the milli-Hartree accuracy, which suggests that the DC method can be very time-consuming as shown later. The total energy for B32 aluminum lithium binary alloy converges at a relatively smaller dimension of the Krylov subspace, while the size of the truncated cluster required for the milli-Hartree accuracy exceeds 250 atoms which is larger than that for the gap systems. For the BCC iron total energy shows a little fluctuation as a function of the dimension of the Krylov subspace, while the milli-Hartree accuracy is reachable using a truncated cluster consisting of 254 atoms. The fluctuation of total energy originates from the density of states in BCC iron, since the density of states for the majority spin possesses a rather sharp peak assigned to the localized d-orbitals near the Fermi energy and this position relative to the Fermi energy can affect largely to the total energy and the magnetic moment. Although no information on whether the system is insulating or metallic is required for the construction of the Green functions Eq. (4), lots of eigenvalues will appear near the Fermi energy in metallic systems. This feature makes the convergence difficult, since the density matrix calculated by Eq. (2) is sensitive to the change in the eigenvalues near the Fermi energy, and the BCC iron is the case. The comparison between the fixed and updated shows that the absolute error by the fixed would be negligible for metallic systems. An important result in the calculations for metallic systems is that a large size of truncated cluster is required to achieve the milli-Hartree accuracy, which suggests that mapping to a smaller Krylov subspace is crucial for the efficient calculation rather than performing a direct diagonalization by the DC method.
For covalent and molecular like systems such as DNA, a small peptide, and a carbon nanotube, the absolute error in the total energy drops to below the milli-Hartree accuracy at a smaller size of truncated cluster compared to those for bulks with a finite gap and metallic systems. However, we see that for DNA and the small peptide being ionic and nonperiodic the total energy converges slowly as a function of the dimension of the Krylov subspace compared to that in homogeneous systems such as carbon, silicon in the diamond structure, BCC lithium, and FCC aluminum, which indicates that higher order moments in Eq. (6) contributes substantially to precise description of the complicated density of states. If a truncated cluster consisting of about 180 atoms is used for molecular systems, the absolute error in the total energy can be below Hartree/atom. In this case the long range contribution should be updated at every SCF step, since the absolute error by the fixed is comparable to the accuracy of Hartree/atom.
Figure 5 shows convergence properties of selected physical quantities. For MnO bulk the proposed method well reproduces the local magnetic moment calculated by the conventional k-space scheme. On the other hand, for BCC iron even the largest size of truncated cluster does not fully converge to that by the k-space scheme, which is attributed to a rather sharp peak near the Fermi energy in the density of states for the majority spin, suggesting that a larger size of truncated cluster is needed for the fully convergent result. The x-component of the largest force on atom in DNA and the dipole moment of the small peptide calculated by the k-space scheme are well reproduced by even a smaller size of the truncated cluster, while the complete convergent results are obtained by updating the long range contribution .
From these convergence properties of the total energy and physical quantities, several trends can be summarized as follows: (1) The size of truncated cluster required for the milli-Hartree accuracy increases in order of molecular systems of which chemical bonds are nearly one-dimensional, bulks with a finite gap, and metallic systems, and rough estimates for the size of the truncated cluster are about 50, 150, and 300 atoms, respectively. (2) In homogeneous systems consisting of a single element the rapid convergence can be obtained at a smaller dimension of the Krylov subspace , while the dimension required for the milli-Hartree accuracy increases as structural randomness and ionicity increase. (3) The absolute error in the total energy by the fixed is about Hartree/atom in most cases, and the magnitude seems to increase slightly as ionicity increases.
3.3 Comparison of O() methods
In Fig. 6 the absolute error in the total energy and the computational time calculated by two O() methods, the proposed and DC methods, are shown as a function of the number of atoms in each truncated cluster for BCC lithium bulk. It is found that two methods are equivalent as regards the accuracy. However, we see that the computational time of the proposed method is remarkably reduced compared to that of the DC method. In the proposed method the dimension of the Krylov subspace and that of the subspace for the approximate inverse of the overlap matrix are 10 % and 40 % of the total number of basis functions in the truncated cluster, respectively. In spite of the considerable reduction of the spanned space, the method gives the same result as that of the DC method, which clearly shows rapid convergence of the proposed method based on the Krylov subspace. Considering the general trends in the convergence properties, in comparison with the DC method, we see that the proposed method is more efficient especially for metallic systems.
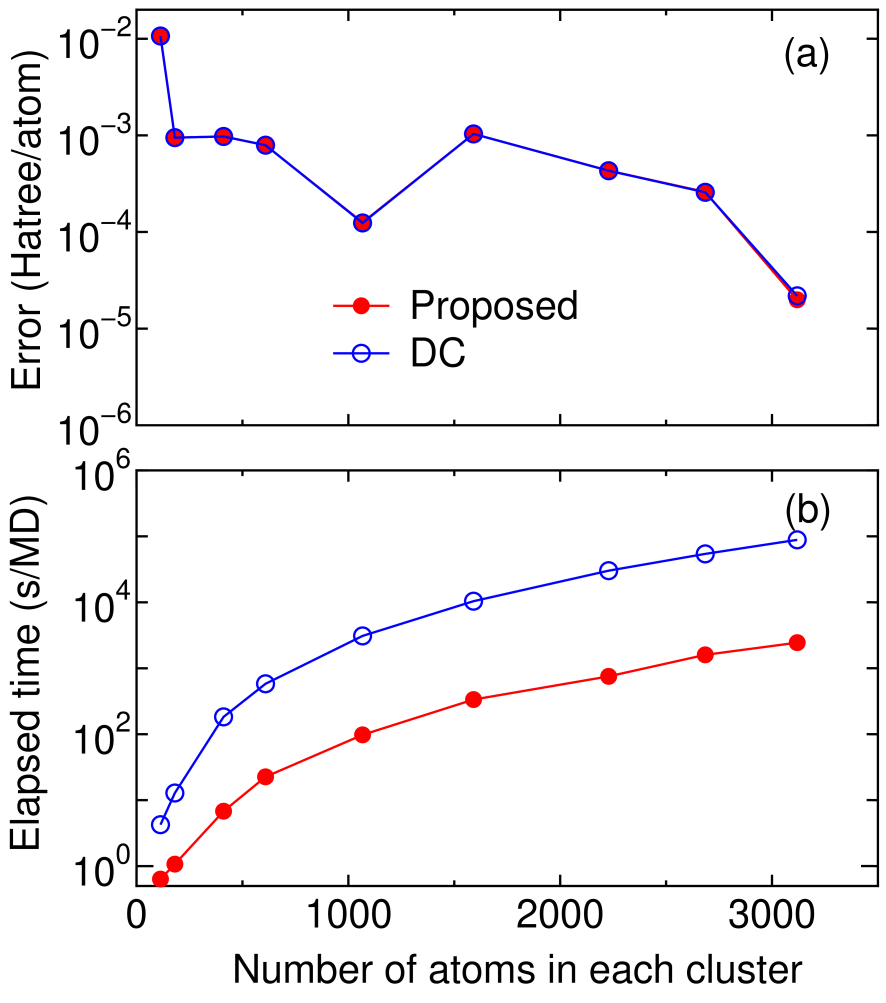
Figure 6: (Color online) (a) absolute error, with respect to a conventional diagonalization scheme, in the total energy (Hartree/atom) for BCC lithium bulk as a function of atoms in each truncated cluster calculated by two linear scaling methods, (b) computational time (s) for the diagonalization part per MD step. The number of atoms in the core region is 113. The dimension of subspaces and are taken as 10 and 40 % of the total number of basis functions in the truncated cluster, respectively. The calculations were performed using one processor of Opteron machine.
To compare the numerical stability, the convergent history of the residual norm in the SCF calculation is shown in Fig. 7 for the conventional k-space diagonalization and four linear scaling methods for FCC aluminum. The residual norm of charge density by the conventional k-space diagonalization, proposed, and DC methods quickly decreases, while the convergent result is hardly obtained in the proposed method with the regeneration of the Krylov subspace and the recursion method. The comparison between the proposed method and its variant with the regeneration of the Krylov subspace suggests a reason why the recursion method tends to suffer from the numerical instability. The regeneration of the Krylov subspace makes the spanned subspace fluctuate, which means that an eigenvalue problem defined by a different subspace is solved at every SCF step. This fluctuation of the spanned space causes the difficulty in obtaining the SCF convergence for the recursion method. On the other hand, in the proposed method without the regeneration of the Krylov subspace the difficulty is avoided since the spanned space is fixed during the SCF calculation.
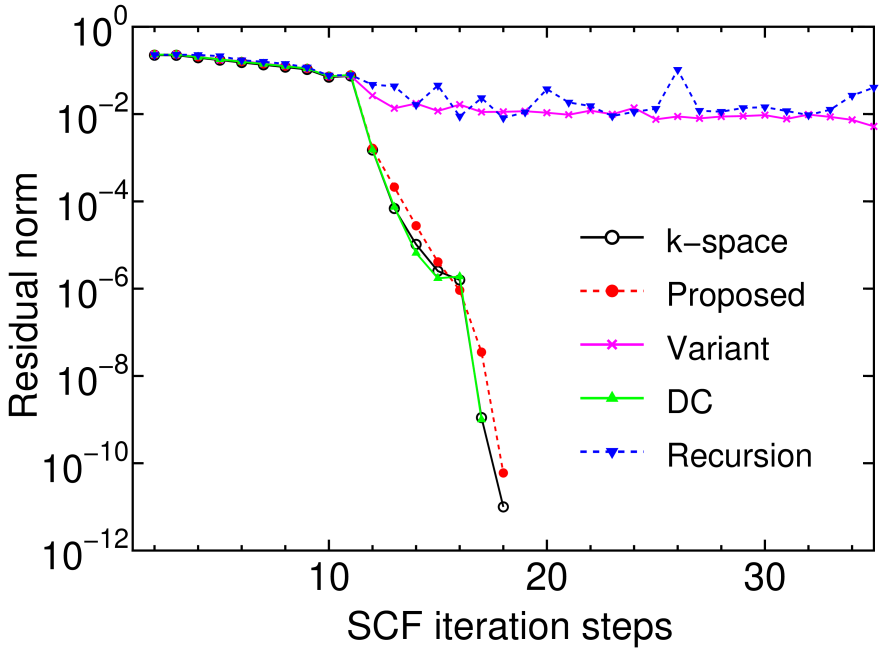
Figure 7: (Color online) The residual norm of charge density as a function of SCF steps calculated by the conventional k-space diagonalization, the proposed, its variant with the regeneration of the Krylov subspace, DC, and recursion methods for FCC aluminum bulk. In the proposed method, the core and buffer regions contain 55 and 242 atoms, respectively. The dimension of subspaces and are taken as 22 and 88 % of the total number of basis functions in the truncated cluster, respectively. After applying a simple mixing method until eleven SCF steps, a residual minimization method-direct inversion in the iterative subspace (RMM-DIIS) is used for later SCF steps.
For diamond carbon the crossing point between the proposed and conventional k-space diagonalization methods with respect to the computational time is about 500 and 250 atoms using 8 and 32 processors, respectively, as shown in Fig. 8. The method can be easily parallelized on a distributed memory parallel machine, since the calculation of each truncated cluster is performed almost independently with a small communication for the calculation of the total number of electrons, suggesting that the parallel efficiency of this method is superior to that of the k-space diagonalization. Therefore, the crossing point is dependent on the number of processors used, and decreases as the number of processors increases as shown in Fig. 8. Since 50 % of the total number of basis functions in the truncated cluster is used for the dimension of Krylov subspace, the computational speed should be times faster than the DC method as far as the computational part for diagonalization, while the actual speed up ratio is 5.8 times in case the super cell containing 1000 atoms is calculated using 32 processors.
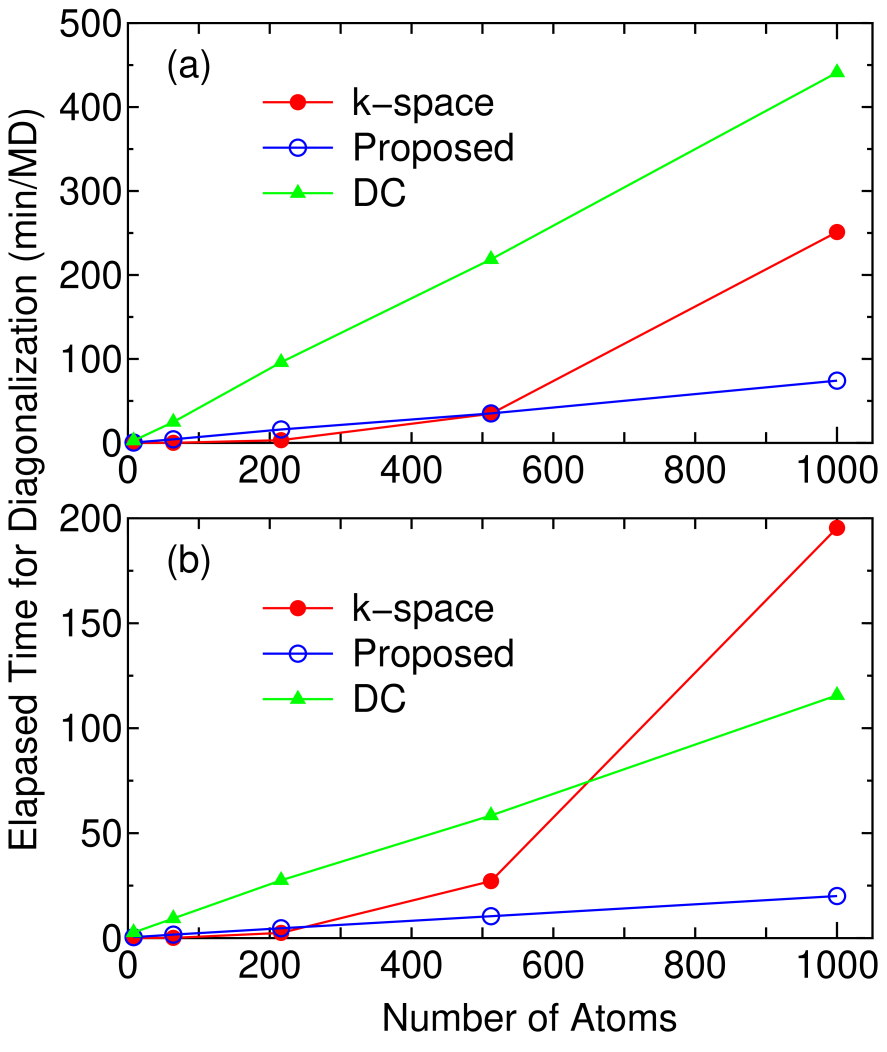
Figure 8: (Color online) The elapsed time for the diagonalization part per MD step calculated by the conventional k-space diagonalization, the proposed, and the DC methods using (a) 8 and (b) 32 processors on an Opteron PC cluster for diamond carbon as a function of the number of atoms in the super cell. For the conventional scheme, only the point was used. For the proposed and DC methods, the number of atoms in the truncated cluster is 159, and in the proposed method the dimension of subspaces and are taken as 50 and 100 % of the total number of basis functions in the truncated cluster, respectively.
4 APPLICATIONS
To illustrate practical aspects in applications of the proposed O() method, we present three applications of the O() methods: (A) calculation of full wave functions of DNA, (B) interaction between a finite carbon nanotube and aluminum surface, and (C) geometry optimization of boron doped diamond.
4.1 Calculation of full wave functions of DNA
Since the proposed method is based on the evaluation of a local Green function rather than wave functions, one cannot obtain full one-particle wave functions of large scale systems from the O() calculation directly. However, the full wave functions can be often useful for gaining an insight into the system and getting information on the phase factor of wave functions. An alternative scheme of obtaining the wave functions is to diagonalize once the whole system by a conventional diagonalization scheme after getting self-consistent charge distribution using the O() method. For the one-shot diagonalization it is a simple but key idea to make use of the self-consistent charge distribution obtained by the O() method.
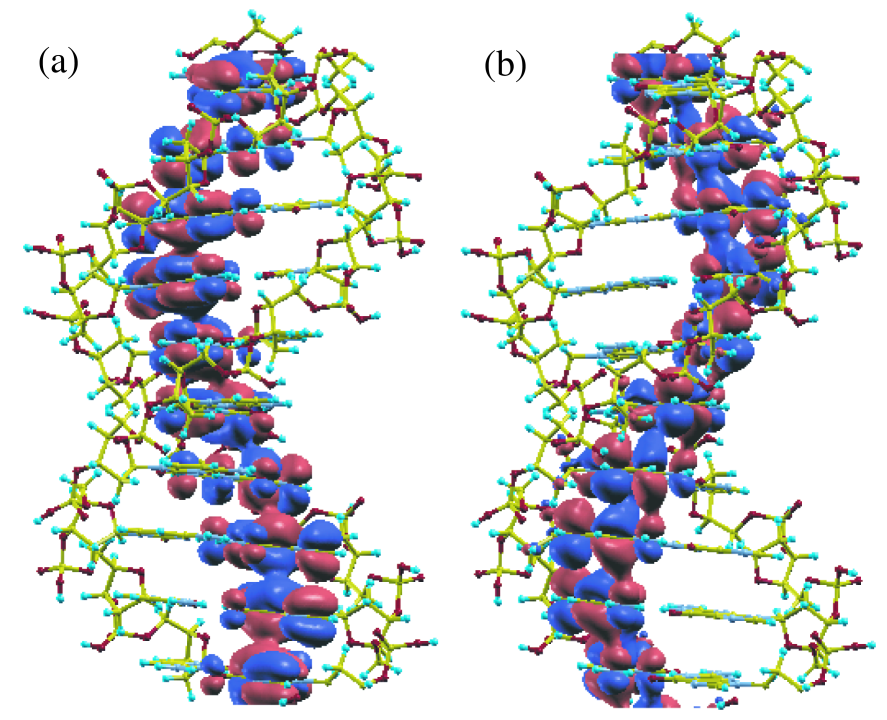
Figure 9: Isosurface maps of (a) the highest occupied (HO) and (b) the lowest unoccupied (LU) state, at the point, of a DNA with a periodic double helix structure (650 atoms/unit) consisting of cytosines and guanines, calculated by the proposed method plus one-shot full diagonalization. The red and blue colors represent the isosurface with plus and minus values, respectively, where an isovalue of 0.007 electron/Bohr is used.
Figure 9 shows the full wave functions calculated by the alternative scheme which correspond to the highest occupied (HO) state and the lowest unoccupied (LU) state, at the point, of the same DNA as discussed in the previous section. For this calculation the cutoff radius to construct a physical truncated cluster is 10.0 Å, and the number of hopping is three for the construction of a logically truncated cluster, giving that the average number of atoms in each truncated cluster is 183. The dimension of the Krylov subspace is 400, and the inverse of overlap matrix is exactly calculated by the Cholesky decomposition instead of the Krylov subspace method. The long range contribution is updated at every SCF step. Under the calculation condition the absolute error, with respect to a conventional diagonalization scheme, in the total energy is 0.000064 Hartree/atom. We see that the HO state consists of guanines and that the LU wave function extends on only cytosines in which two parallel guanines (cytosines) form a bonding state in the HO (LU) state. No significant contribution from the backbone consisting of pentoses connected with phosphodiester linkage is found for both the states. The feature originates from the HO state, located at a relatively higher energy, of a guanine molecule and the low lying LU state of a cytosine molecules.[47, 48] A comparison on the DOS between the alternative scheme and a conventional diagonalization method in which the calculation was performed self-consistently using the conventional diagonalization method from the beginning is shown in Fig. 10. The alternative scheme well reproduces the DOS calculated by the conventional scheme for a wide range of energy, supporting that the proposed O() method is accurate enough for assuring the validity of the alternative scheme of calculating the full wave functions.
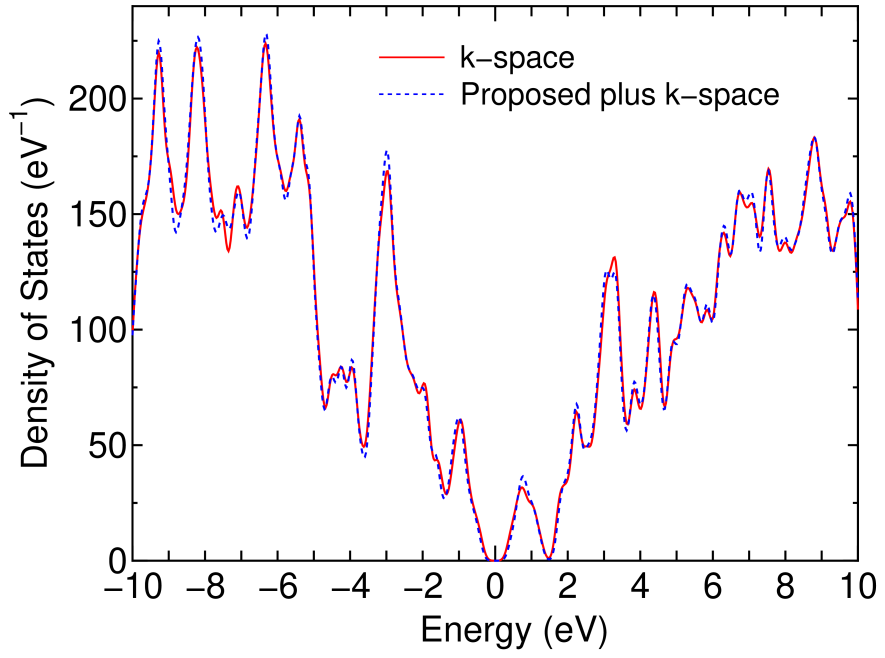
Figure 10: (Color online) Density of states of the same DNA as in Fig. 9, calculated by the conventional k-space diagonalization with only the point and the proposed method plus one-shot full diagonalization. The discrete spectrum is smeared out using a Gaussian broadening method with a width of 0.15 eV.
4.2 Interaction between a carbon nanotube and metal surface
A significant aspect of the proposed method is that metallic systems can be treated on the same footing as for systems with a finite gap. To illustrate the capability, we show a calculation on interaction between a finite sized CNT and aluminum surface. A (10,0) zigzag carbon nanotube we considered consisting of 339 carbon atoms with a finite length of 35 Å possesses dangling bonds introduced by the chopping at both the edges which are expected to exhibit local magnetic moments. No hydrogen passivation is made at both the edges. In addition, a defect, generated by removing a carbon atom, is introduced at the central region with respect to the long axis and the counter side of that of CNT facing the aluminum surface. Carbon atoms around this defect may also exhibit a local magnetic moment due to the dangling bonds. The structure of CNT is constructed by assuming that all the bond lengths between two carbon atoms are 1.42 Å. The aluminum surface we considered consists of cubic cells with a lattice constant 4.05 Å, each of which contains four aluminum atoms, thus totally it contains 768 aluminum atoms. The CNT is placed along [100] axis on the (001) surface so that some of carbon atoms facing the surface can be on top of the aluminum atoms consisting of the (001) surface with an interatomic distance of 2.0 Å between the carbon and aluminum atoms. For both the structures of the CNT and the aluminum surface no optimization is performed. The total composite system is treated as a slab model of which unit cell volume is . For the proposed method the cutoff radius to construct a physical truncated cluster is 11.0 Å, and the number of hopping is three for the construction of a logically truncated cluster. The dimension of the Krylov subspace is 800, and the inverse of overlap matrix is exactly calculated by the Cholesky decomposition instead of the Krylov subspace method. The long range contribution is updated at every SCF step. Under the calculation condition the absolute error, with respect to a conventional diagonalization scheme, in the total energy is 0.00443 and 0.00014 Hartree/atom for FCC aluminum and a periodic (10,0) carbon nanotube without the edges, respectively. For a comparison between the proposed and the conventional methods we also performed a conventional k-space calculation with only the point for the same composite system. The elapsed time for the diagonalization part is about 19 and 185 minutes per SCF step for the proposed method and the conventional diagonalization, respectively, using 45 Opteron processors.
Figure 11(a) shows an isosurface map of spin charge density and a profile of charge density along a line denoted by an arrow in the composite system. A comparison between the proposed and the conventional k-space methods in the profile of charge density shows that the proposed method reproduces very accurately the spatial charge distribution in the vicinity of not only the CNT, but also the metallic slab. Large magnetic moments can be found around the edges of CNT and the neighboring carbon atoms to the defect. Although the magnetic moment around the edges is mainly attributed to the dangling bonds corresponding to lone pair electrons in the most outside atoms, the relatively inner atoms without the dangling bond also exhibit considerable magnetic moments in which the local spins are ferro magnetically ordered along the circumference and anti ferro magnetically ordered between two circumferences. This feature is consistent with a result by the other DFT calculation,[49] showing the spin polarization of electrons at near the zigzag edge in a finite sized zigzag CNT with hydrogen passivation.
| Carbon site | Charge | Spin moment | ||
|---|---|---|---|---|
| O() | Conventional | O() | Conventional | |
| C | 4.032 | 4.029 | 1.264 | 1.280 |
| C | 4.028 | 4.033 | 1.259 | 1.224 |
| C | 4.036 | 4.038 | 1.178 | 1.168 |
| C | 4.047 | 4.051 | 1.115 | 1.121 |
| C | 4.147 | 4.142 | 0.367 | 0.512 |
| C | 4.005 | 4.005 | -0.148 | -0.149 |
| C | 4.004 | 4.004 | -0.146 | -0.144 |
| C | 4.003 | 4.003 | -0.135 | -0.133 |
| C | 4.008 | 4.007 | -0.121 | -0.122 |
| C | 4.005 | 4.005 | -0.091 | -0.105 |
| C | 4.145 | 4.144 | -0.069 | -0.081 |
| C | 4.039 | 4.036 | 0.656 | 0.659 |
| C | 4.040 | 4.036 | 0.645 | 0.657 |
| C | 3.997 | 3.995 | -0.364 | -0.373 |
The magnetic moments of the most outside atoms labeled by C-C and the next inner atoms labeled by C-C are listed in Table 1, where C and C are the most distant carbon atom in the circumferences from the aluminum surface, C and C are the closest ones, and the other ones are in between the former and the latter. The magnetic moments of the most outside atoms and the next inner atoms are about 1.2 and 0.13 (), respectively, while they vary depending on the relative position to the aluminum surface. The magnetic moment of neighboring atoms to the defect is much smaller than that of the most outside atoms in spite of the existence of lone pair electrons. In addition, the same trend as in the edge regions is found in the magnetic ordering between two circumferences, i.e., two local spins of C and C siting in the same circumference are ferro magnetically ordered and anti ferro magnetic ordering is observed between atoms C and C or C and C in two circumferences. The decrease in the magnetic moment of the neighboring atoms to the defect may be attributed to the decrease in the number of neighboring atoms with a dangling bond in the same circumference, which may contribute to the enhancement of the ferro magnetic ordering. However, a further study will be needed for a conclusive understanding on the magnitude of magnetic moments. A comparison between the proposed and the conventional k-space methods in the Mulliken charge and spin moment listed in Table 1 clearly shows the accuracy of the proposed method. The Mulliken charge is highly accurately reproduced with an absolute error of 0.005 at most, while the error with respect to the conventional k-space result in the spin moment tends to be larger than that for the Mulliken charge.
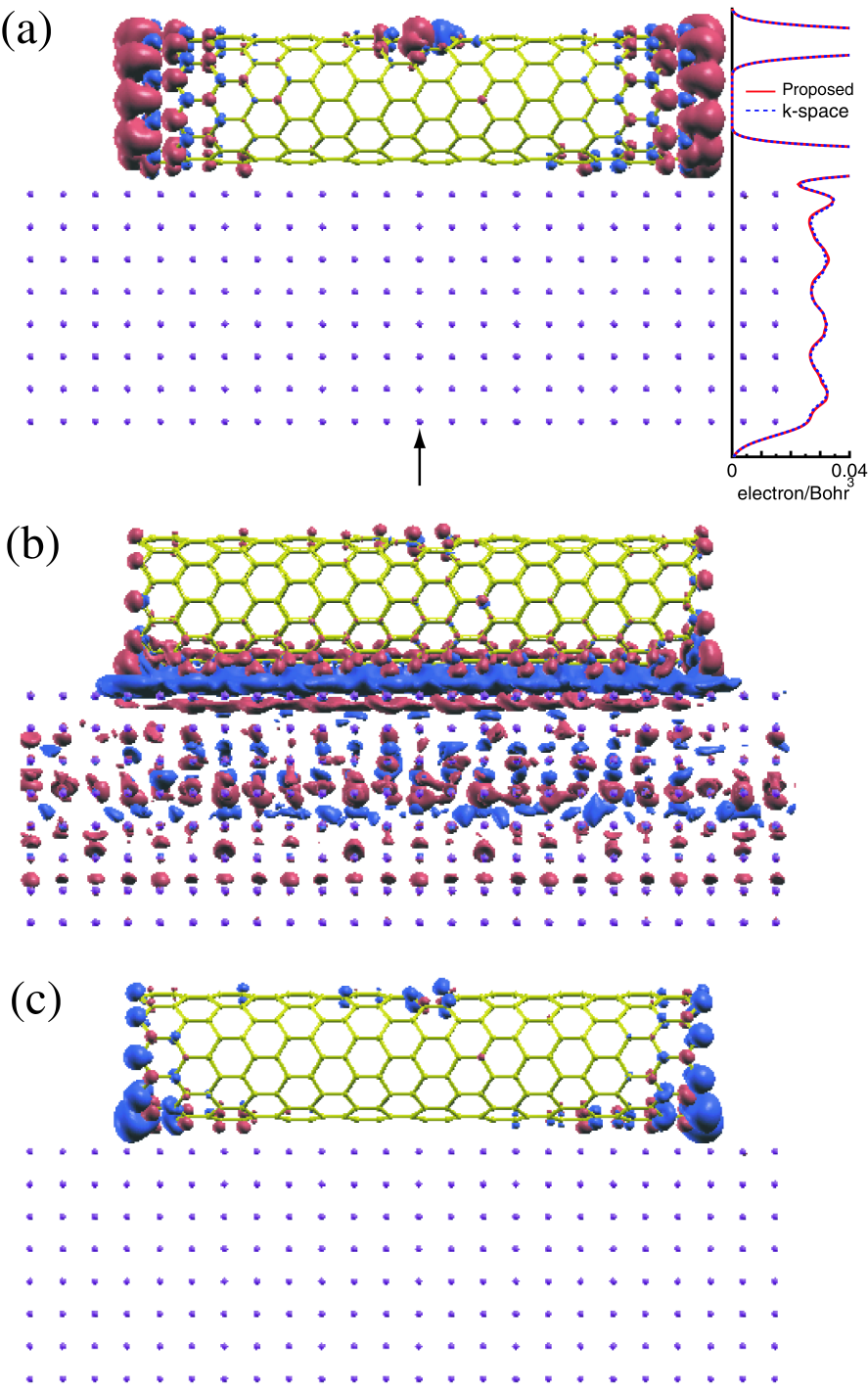
Figure 11: (a) Isosurface map of spin charge density for a (10,0) finite sized zigzag carbon nanotube on aluminum surface and a profile of charge density along a line denoted by an arrow which points the center of the plane perpendicular to the paper. Isosurface maps of (b) difference charge density and (c) difference spin density, where the difference charge (spin) density is defined as the difference between the composite system and the sum of the isolated CNT and the slab with respect to the charge (spin) density. The small gray circles denote aluminum atoms. The red and blue colors represent the isosurface with plus and minus values, respectively, where an isovalue of 0.0018 electron/Bohr is used for all the cases.
Isosurface maps of the difference charge density and difference spin density are shown in Figs. 11(b) and (c), respectively, where the difference charge (spin) density is defined as the difference between the composite system and the sum of the isolated CNT and the slab with respect to the charge (spin) density. We see that electrons in the region just above the aluminum surface transfer to the region around the bottom of the CNT corresponding to the side facing to the aluminum surface, the most outside atoms, and the peripheral atoms to the defect. The charge transfer between the region just above the aluminum surface and the region around the bottom of the CNT can be regarded as a typical Ohmic contact. On the other hand, the charge transfer into atoms with the dangling bond can be considered as a charge doping to impurity states lying between the valence and conduction states, while the magnitude of charge transfer decreases rapidly as the distance between the carbon and the surface increases. Another interesting finding is a Friedel oscillation in the difference charge density, i.e., the increase and decrease of charge density appear alternatively along the depth direction in the aluminum slab, which suggests that the composite system cannot be modeled by a thin slab. Also we see that the charge doping to dangling bonds depresses the magnetic moment as shown in Fig. 11(c), indicating that the states for the minority spin locate just above those of the majority spin.
| O() | Conventional | E | |
|---|---|---|---|
| CNT | -1941.39378 | -1941.41657 | 0.02279 |
| Al slab | -37136.19912 | -37136.86054 | 0.66142 |
| CNT + Al slab | -39077.59289 | -39078.27711 | 0.68421 |
| CNT on Al slab | -39077.29141 | -39078.07384 | 0.78243 |
| (CNT on Al slab)-(CNT + Al slab) | |||
| 0.30148 | 0.20327 | 0.09822 | |
Table 2 shows the total energies of the isolated CNT, the aluminum slab, and the composite system calculated by the proposed O() method and the conventional diagonalization scheme. For the isolated CNT the absolute error with respect to the conventional diagonalization in the total energy is about 0.02 Hartree (0.00006 Hartree/atom), while that for the aluminum slab is 0.00086 Hartree/atom which is fourteen times larger than the former. The interaction energy between the CNT and the aluminum slab is calculated as 0.301 and 0.203 Hartree by the proposed method and the conventional diagonalization, respectively. Although there is a cancellation of the error in the calculation of the interaction energy, the absolute error in the interaction energy is 0.098 Hartree (2.7 eV), and it is not negligible, which suggests that a further severe calculation condition is needed for a more accurate calculation of this composite system. Also the positive interaction energy implies importance of the geometry optimization to treat the interaction of the composite system properly. The further study and the details will be discussed elsewhere.
4.3 Geometry optimization of boron doped diamond
The force on atom calculated by the proposed O() method is not derived from a variational principle, but evaluated by employing an expression based on the Hellman-Feynman theorem with a Pulay correction which can be variationally derived only if the eigenvalue problem is exactly solved. Thus, the force is not consistent with the total energy within the proposed O() method unless a infinitely large truncated cluster is used, which can be a disadvantage in the method. However, if the calculated forces are accurate enough so that the geometry optimization can be converged within a criterion of Hartree/Bohr, such a geometry optimization may be applicable to a wide variety of problems in a practical sense. Along this line a geometry optimization by the proposed O() method is demonstrated for boron doped diamond of which super cell contains 62 carbon atoms and two boron atoms being nearest neighbors.[50] The lattice constant of 3.567 Å is used, and the unit cell is fixed during the relaxation. Figure 12 shows the absolute maximum force on atom in the geometry optimization as a function of the optimization steps, calculated by a conventional k-space diagonalization and the proposed O() method with four calculation conditions in which the number of atoms in each truncated cluster is 159, 275, 381, and 525, and the dimension of the Krylov subspace is 425, 800, 1100, and 1600 for Krylov1, Krylov2, Krylov3, and Krylov4, respectively, and for all the cases the long range contribution is updated at every SCF step, and the inverse of overlap matrix is exactly calculated by the Cholesky decomposition. It is found that the absolute maximum force by the proposed O() method fluctuates after converging at a certain level ranging from to Hartree/atom which implies the error in the force calculated by the proposed O() method, while in the conventional scheme it converges rapidly. The error in the force decreases as the number of atoms in the truncated cluster and the dimension of the Krylov subspace increase, and the criterion of Hartree/Bohr is satisfied in the most severe condition we studied.
| Krylov1 | Krylov2 | Krylov3 | Krylov4 | k-space | |
|---|---|---|---|---|---|
| r(BB) | 1.975 | 1.977 | 1.983 | 1.988 | 1.990 |
| r(BC) | 1.544 | 1.544 | 1.543 | 1.544 | 1.543 |
| r(CC) | 1.567 | 1.568 | 1.568 | 1.568 | 1.568 |
| (BBC) | 100.60 | 100.57 | 100.52 | 100.40 | 100.37 |
| (CBC) | 116.64 | 116.72 | 116.74 | 116.81 | 116.83 |
| E | 0.0644 | 0.0625 | 0.0576 | 0.0615 | 0.0626 |
As shown in Table 3 selected bond lengths, bond angles, and the relaxation energy obtained by the proposed method converge to those by the conventional k-space scheme as the calculation condition becomes severe, and the most severe condition Krylov4 almost reproduces the k-space results. Thus, for practical purposes it is possible to perform the geometry optimization using the proposed O() method with a careful attention to the accuracy.
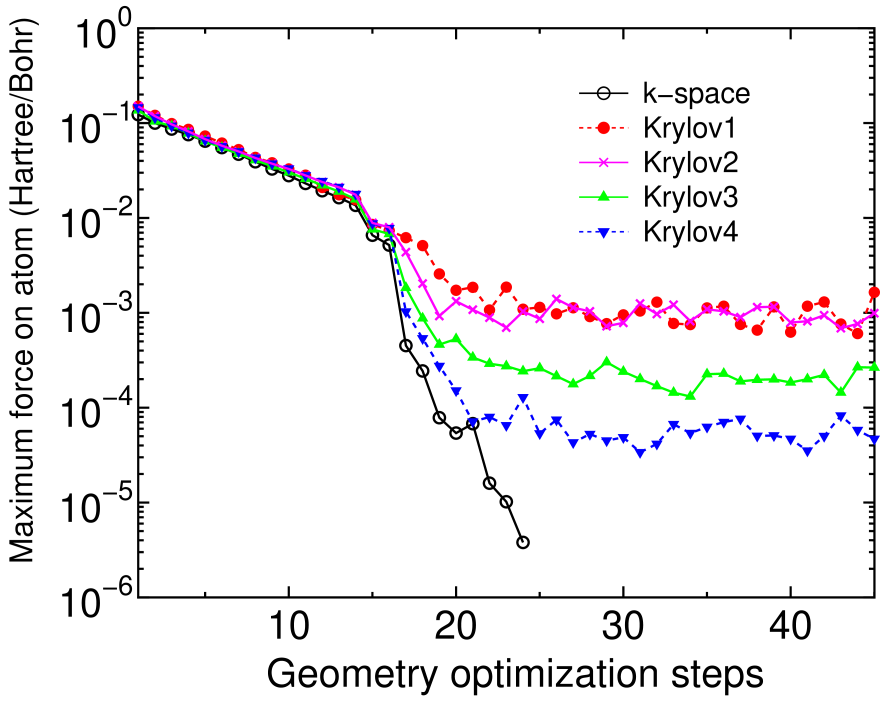
Figure 12: (Color online) The absolute maximum force on atom in the boron doped diamond as a function of the geometry optimization steps. For the calculation conditions of the proposed O() method see text. After applying a steepest descent (SD) method until fourteen optimization steps, the RMM-DIIS for geometry optimization is used for later steps.
5 CONCLUSIONS
To conclude, we have developed an efficient and robust O() method based on a Krylov subspace for fully self-consistent large scale ab initio electronic structure calculations of a wide variety of materials including metals. Based on the Krylov subspace an embedded cluster problem is solved with an effective Hamiltonian consisting of the detailed short range and the effective long range contributions. The charge flow between embedded clusters is taken into account by introducing a common chemical potential, and also the long rang Coulomb interaction is properly included by solving the Poisson equation for the whole system. The method can be regarded as a unified approach connecting the DC and recursion methods, and enables us to obtain convergent results with the milli-Hartree accuracy for a wide variety of materials. The almost independent calculation for each truncated cluster assures easiness of the parallel implementation and the high parallel efficiency.
The accuracy and efficiency of the method are mainly controlled by two parameters, the size of the truncated cluster and the dimension of the Krylov subspace, and the optimum choice depends on the system under consideration. A systematic study for the convergence properties of the total energy and physical quantities provides a practical guidelines for adjusting the accuracy and efficiency: (1) the milli-Hartree accuracy can be achieved by the truncated cluster including about 50, 150, and 300 atoms for molecular systems, bulks with a finite gap, and metallic systems, respectively, which can be a minimum size of truncated cluster. (2) In most cases the convergent result for a given truncated cluster can be obtained by less than 50% of the total number of basis functions in the truncated cluster for the dimension of the Krylov subspace, which means that the proposed O() method is faster than the DC method, while the dimension required for the milli-Hartree accuracy increases as structural randomness and ionicity increase.
The applications of the O() method to three examples, (A) calculation of full wave functions of DNA, (B) interaction between a carbon nanotube and metal surface, and (C) geometry optimization of boron doped diamond, show that the O() method can be applicable even for a composite system including metallic systems with considerable accuracy. However, it should be noted that the required accuracy depends on the physical quantity under consideration, and that a careful consideration to the convergence property of the physical quantity is indispensable before performing large scale calculations. With the careful consideration it can be concluded that the proposed O() method is a quite promising approach for realization of large scale ab initio electronic structure calculations for a wide variety of materials.
Acknowledgments
The author would like to thank Prof. K. Terakura for his continuous encouragement. The author was partly supported by CREST-JST and NAREGI Nanoscience Project, the Ministry of Education, Science, Sports, and Culture, Japan. Part of the computation in this work was done using the computational facilities of the Japan Advanced Institute of Science and Technology (JAIST).
Appendix A Appendix
In the Appendix we show that it is possible to minimize the computational time in the DC method by optimizing the size of the central region that the associated Green functions are evaluated. The argument with a little modification holds even for the Krylov subspace method proposed in this paper. In the original DC method [4] only the Green functions associated with the single central site are evaluated using Eq. (4). However, instead of the single site one can adopt the clustered sites including multiple sites as the central region that the associated Green functions are evaluated. In this generalization to the central region, there is an optimum size of the central region to minimize the computational time as shown by the following simple consideration: In the conventional diagonalization the computational time is given by
| (A.1) |
where is a prefactor, the number of sites in the whole system, and it is assumed that all the sites contain a single basis function and that only the point is taken into account. On the other hand, the computational time of the generalized DC (GDC) method can be estimated for a uniform system by
| (A.2) |
where is the number of the sites in the central region that the associated Green functions are evaluated, the number of remaining sites in the buffer region. It it noted that the central and buffer regions used here are different from those depicted by Fig. 1. Since the total number of sites in the truncated cluster is the sum of and and the number of the truncated cluster is , provided that the Green functions associated with the central region are evaluated in the calculation of the each truncated cluster, the computational time should scale as the third power of and be proportional to the number of truncated clusters . Then, considering , an optimum number of the central sites is given by
| (A.3) |
Thus, we find a simple relation that the computational time can be minimized when is a half of . Substituting Eq. (A.3) into Eq. (A.2) and noting and , we have
| (A.4) |
Compared to the original DC method we see that the order of in the prefactor is reduced from three to two. Equating with the crossing point between the GDC method and the conventional diagonalization with respect to the computational time is written by
| (A.5) |
It is found that the crossing point is proportional to the number of sites in the truncated cluster, while that for the original DC method scales as . It is noted that the above discussion holds for a system with any dimensionality and that the same conclusion can be also obtained by chain, square, and cubic tight binding lattice models with a little approximation. However, how the whole system can be divided into a set of the central regions depends on the dimensionality of the system. Although for one dimensional systems it is rather straightforward to make the spatial division, it brings another difficult problem for higher dimensional systems with inhomogeneous atomic arrangement. A study toward this direction will be a future work.
References
- [1] P. Hohenberg and W. Kohn, Phys. Rev. 136, B 864 (1964); W. Kohn and L. J. Sham, ibid. 140, A 1133 (1965).
- [2] S. Goedecker, Rev. Mod. Phys. 71, 1085 (1999) and references therein.
- [3] S. Goedecker and G.E. Scuseria, Comp. Sci. Eng. 5, 14 (2003).
- [4] W. Yang, Phys. Rev. Lett. 66, 1438 (1991); W. Yang and T. Lee, J. Chem. Phys. 163, 5674 (1995); J. Khandogin, K. Musier-Forsyth, and D.M. York, J. Mol. Biol. 330, 993 (2003).
- [5] D. G. Pettifor, Phys. Rev. Lett. 63, 2480 (1989); ibid. M. Aoki, 71, 3842 (1993); A.P. Horsfield, A.M. Bratkovsky, D.G. Pettifor, and M. Aoki, Phys. Rev. B 53, 1656 (1996).
- [6] G. Galli and M. Parrinello, Phys. Rev. Lett. 69, 3547 (1992).
- [7] X.-P. Li, R.W. Nunes, and D. Vanderbilt, Phys. Rev. B 47, 10891 (1993).
- [8] M.S. Daw, Phys. Rev. B 47, 10895 (1993).
- [9] P. Ordejon, D.A. Drabold, M.P. Grumbach, and R.M. Martin, Phys. Rev. B 48, 14646 (1993); P. Ordejon, D.A. Drabold, R.M. Martin, and M.P. Grumbach, ibid. 51, 1456 (1995).
- [10] D.R. Bowler and M.J. Gillan, Comp. Phys. Comm. 120, 95 (1999); D.R. Bowler and M.J. Gillan, Chem. Phys. Lett. 355, 306 (2002); T. Miyazaki, D.R. Bowler, R. Choudhury, and M.J. Gillan, J. Chem. Phys. 121, 6186 (2004).
- [11] C.-K. Skylaris, A.A. Mostofi, P.D. Haynes, O. Dieguez, and M.C. Payne Phys. Rev. B 66, 035119 (2002); A.A. Mostofi, P.D. Haynes, C.-K. Skylaris, and M.C. Payne, J. Chem. Phys. 119, 8842 (2003); C.-K. Skylaris, P.D. Haynes, A.A. Mostofi, and M.C. Payne, ibid. 122, 084119 (2005).
- [12] S. Goedecker and L. Colombo, Phys. Rev. Lett. 73, 122 (1994); S. Goedecker and M. Teter, Phys. Rev. B 51, 9455 (1995).
- [13] L. Seijo and Z. Barandiaran, J. Chem. Phys. 121, 6698 (2004).
- [14] T. Ozaki and K. Terakura, Phys. Rev. B 64, 195126 (2001).
- [15] T. Ozaki, Phys. Rev. B 59, 16061 (1999); T. Ozaki, M. Aoki, and D.G. Pettifor, ibid. 61, 7972 (2000).
- [16] R. Takayama, T. Hoshi, and T. Fujiwara, J. Phys. Soc. Jpn. 73, 1519 (2004).
- [17] R. Takayama, T. Hoshi, T. Sogabe, S.-L. Zhang, T. Fujiwara, Phys. Rev. B 73, 165108 (2006).
- [18] Y. Wang, G.M. Stocks, W.A. Shelton, and D.M.C. Nicholson, Z. Szotek, and W.M. Temmerman, Phys. Rev. Lett. 75, 2867 (1995).
- [19] A.V. Smirnov and D.D. Johnson, Phys. Rev. B 64, 235129 (2001).
- [20] R. Baer and M. Head-Gordon, Phys. Rev. B 58, 15296 (1998).
- [21] A.D. Daniels and G.E. Scuseria, J. Chem. Phys. 110, 1321 (1999).
- [22] K. Kitaura, E. Ikeo, T. Asada, T. Nakano, M. Uebayasi, Chem. Phys. Lett. 313, 701 (1999); K. Kitaura, S.-I. Sugiki, T. Nakano, Y. Komeiji, M. Uebayasi, Chem. Phys. Lett. 336, 163 (2001); D.G. Fedorov and K. Kitaura, Chem. Phys. Lett. 389, 129 (2004); D. G. Fedorov, T. Ishida, K. Kitaura, J. Phys. Chem. A. 109, 2638 (2005).
- [23] R. Haydock, V. Heine, and M.J. Kelly, J. Phys. C 5, 2845 (1972); 8, 2591 (1975); R. Haydock, Solid State Phys. 35, 216 (1980).
- [24] G. Galli and F. Mauri, Phys. Rev. Lett. 73, 3471 (1994).
- [25] A. Canning, G. Galli, and J. Kim, Phys. Rev. Lett. 78, 4442 (1997).
- [26] T. Ozaki, Y. Iwasa, and T. Mitani, Phys. Rev. Lett. 84, 1712 (2000).
- [27] J.M. Millam and G.E. Scuseria, J. Chem. Phys. 106, 5569 (1997).
- [28] G. E. Scuseria, J. Phys. Chem. A 103, 4782 (1999).
- [29] K. Nemeth and G.E. Scuseria, J. Chem. Phys. 113, 6035 (2000).
- [30] Z. Bai, J. Demmel, J. Dongarra, A. Ruhe and H. van der Vorst, editors, Templates for the solution of Algebraic Eigenvalue Problems: A Practical Guide. SIAM, Philadelphia, 2000.
- [31] T. Ozaki, Phys. Rev. B. 67, 155108 (2003); T. Ozaki and H. Kino, ibid. 69, 195113 (2004).
- [32] E. Tsuchida and M. Tsukada, Phys. Rev. B 54, 7602 (1996).
- [33] T. Ozaki and H. Kino, Phys. Rev. B. 72, 045121 (2005).
- [34] T. Ozaki, Phys. Rev. B 64, 195110 (2001).
- [35] In case of , the eigenvalue problem Eq. (3) becomes equivalent to that derived variationally from the total energy, and the resultant Green function becomes exact. Otherwise, the eigenvalue problem Eq. (3) is not derived variationally from the total energy functional.
- [36] Strictly speaking, the block element can contain informations of ()th moments in case a set of vectors as the initial state is used, where is the number of vectors in the initial state. Thus, the Green function contains up to ()th moments in this case.
- [37] D. Kincaid and W.Cheney, Numerical Analysis (Brooks/Cole, 1996).
- [38] C.M.M. Nex, J. Phys. A: Math. Gen 11, 653 (1978).
- [39] The code, OpenMX, pseudo-atomic basis functions, and pseudopotentials are available on a web site (http://staff.aist.go.jp/t-ozaki/).
- [40] N. Troullier and J.L. Martins, Phys. Rev. B 43, 1993 (1991).
- [41] P.E. Blochl, Phys. Rev. B 41, 5414 (1990).
- [42] J.P. Perdew, K. Burke, and M. Ernzerhof, Phys. Rev. Lett. 77, 3865 (1996).
- [43] J.M. Soler, E. Artacho, J.D. Gale, A. Garcia, J. Junquera, P. Ordejon, and D. Sanchez-Portal, J. Phys.: Condens. Matter 14, 2745 (2002).
- [44] A.D. MacKerell, M. Feig, and C.L. Brooks, J. Comput. Chem. 25, 1400 (2004).
- [45] A. Goldstein, S. Tachibana, L.I. Lowney, M. Hunkapiller, and L. Hood, Proc. Natl. Acad. Sci. U. S. A. 76, 6666 (1979).
- [46] P. Ren and J.W. Ponder, J. Comput. Chem. 23, 1497 (2002).
- [47] X. Yang, X.-B. Wang, E.R. Vorpagel, and L.-S. Wang, Proc. Natl. Acad. Sci. USA 101, 17588 (2004);
- [48] M. Taniguchi and T. Kawai, Phys. Rev. E 70, 011913 (2004).
- [49] S. Okada and A. Oshiyama, J. Phys. Soc. Jpn. 72, 1510 (2003).
- [50] J.P. Goss, P.R. Briddon, R. Jones, Z. Teukam, D. Ballutaud, F.Jomard, J. Chevallier, M. Bernard, and A. Deneuville, Phys. Rev. B 68, 235209 (2003).