Orbital Optimization Method: Ver. 1.0
The original has been published
in Phys. Rev. B 67, 155108 (2003).
Abstract
A simple and practical method for variationally optimizing numerical atomic orbitals used in density functional calculations is presented based on the force theorem. The derived equation provides the same procedure for the optimization of atomic orbitals as that for the geometry optimization. The optimized orbitals well reproduce convergent results calculated by a larger number of unoptimized orbitals. In addition, we demonstrate that the optimized orbitals significantly reduce the computational effort in the geometry optimization, while keeping a high degree of accuracy.
1 INTRODUCTION
During the last decade, to extend the applicability of density functional theories (DFT) to realistic large systems, great efforts have been done for developing O() methods of the eigenvalue problem [1, 2, 3, 4, 5, 6] and for making efficient and accurate localized orbitals [7, 8, 9, 10] as a basis set being suitable for O() methods. Among these studies, one of important and unresolved problems is how atomic orbitals as a basis set are constructed to maximize both the computational efficiency and accuracy. One expects that a basis set such as double valence orbitals with polarized orbitals for valence electrons provides a way for balancing a relatively small computational effort and a considerable degree of accuracy. Along this line, accurate basis sets were constructed in several ways [7, 8, 9, 10]. Kenny et al. constructed a basis set, so that atomic orbitals span the subspace defined by selected and occupied states of reference systems as much as possible [7]. Junquera et al. optimized the shape and cutoff radii of atomic orbitals for reference systems by using the downhill simplex method [8]. However, the transferability of these optimized orbitals might be restricted to systems similar to the reference systems used for the optimization in terms of atomic environments and states such as the coordination number and the charge state. A more complete treatment is to optimize atomic orbitals of each atom located on different environments in a given system [10]. In addition, the complete optimization procedure should be simple and efficient practically. In this paper, to overcome the difficulty, we present a simple and practical method, based on the force theorem, for variationally optimizing numerical atomic orbitals of each atom in a given system.
2 VARIATIONAL OPTIMIZATION
Let us expand a Kohn-Sham (KS) orbital of a given system using numerical atomic orbitals in a form of linear combination of atomic orbitals (LCAO):
| (1) |
where is a site index, an organized orbital index, and . For simplicity we consider only nonspin-polarized systems and an non-Bloch expression of the one-particle wave functions, but the extentions of the below description to spin-polarized systems and Bloch wave functions are straightforward. Note that a radial wave function depends on not only an angular momentum quantum number , but also a site index , a multiplicity index , and a magnetic quantum number . To give a variational degree of freedom of , we furthermore expand using primitive orbitals as follows:
| (2) |
where , in which the indices and denote the same as those of the index , and . Note that a primitive radial wave function , which is discussed later on, is independent on , and that the coefficients are independent variables on the eigenstate . Substituting Eq. (2) into Eq. (1), we have
| (3) |
Although the expansion of a KS orbital by Eq. (3) is linearized for each variable or , however, the primitive orbitals are expanded by the product of two variables and in a nonlinearized form. Therefore, it is difficult to directly find the minimum of the KS total energy for the ground state with respect to and as a generalized eigenvalue problem which can be derived in the usual LCAO. To avoid the difficulty, here, we propose a two step optimization scheme, in which the coefficients are optimized after are determined with a set of fixed . Considering for the KS total energy with the orthonormalization relation among one-particle wave functions and fixed contraction coefficients , we have a well-known KS matrix equation with respect to the coefficient as follows:
| (4) |
where is a KS Hamiltonian, and is a KS eigenvalue of the system. There is no restriction to solve Eq. (4) or to find . So, we can use any solution method which could be an exact diagonalization method, iterative methods such as Car-Parinello (CP) method [11] and conjugate gradient (CG) method [12], and O() methods. On the other hand, regarding as dependent variables on and assuming that the Kohn-Sham equation is solved self-consistently with respect to , we can derive the following equation based on the force derivation of non-orthogonal orbitals as follows:
| (5) | |||||
where is an occupancy number for the eigenstate , a bond-order, and an energy bond-order. The final equation in Eq. (5) is derived by taking into account Eq. (4) and the orthonormalization relation . It should be noted that Eq. (5) excludes any derivative, and that and only have to be evaluated for the contracted atomic orbital in Eq. (5), which implies that additional computational costs are not required to evaluate Eq. (5). Once we obtain a self-consistent solution of the Kohn-Sham equation, Eq. (4), with a set of given coefficients , then Eq. (5) gives the gradient of with respect to within small computational costs. This fact shows apparently that the atomic orbitals can be optimized variationally in the same two step procedure as that of the geometry optimization in terms of instead of atomic positions. Therefore, the contraction coefficients are optimized iteratively, coupled with the self-consistent solution of Eq. (4), as follows:
| Step 1 | ||||
| Step 2 | ||||
where an optimum is determined, so that the norm of the gradients at ,
| (7) |
becomes a minimum with respect to under the fixed and . Substituting Eqs. (5) and (2) into Eq. (7), and considering with the fixed and , we have for the minimum of with
| (8) | |||||
| (9) |
where
| (10) |
with and . Taking into account the sparseness of both the Hamitonian and overlap matrices in the real space, we find that the computational efforts to evaluate Eqs. (8) and (9) scale linearly. Therefore, we can easily evaluate , leading no intensive computational demands. After achieving the self-consistent field (SCF) for Eq. (4) with respect to the coefficients by an usual SCF procedure, the contraction coefficients are updated by Eq. (2) and renormalized so that is normalized. Thus, the two step optimization scheme enables us to optimize the contraction coefficients along the stationary minimum line of the KS total energy functional with respect to , while keeping . It is found that about five iterative procedures of the two step optimization, which includes the solution of Eq. (4) and the optimization of by Eq. (2), are enough to accomplish a sufficient convergence of for our test systems. Again it should be mentioned that the bond-order and the energy bond-order are required for only the contracted atomic orbital in Eq. (5). This is a crucial point to make our optimization procedure efficient, since the Kohn-Sham equation based on Eq. (4) can be solved for not large , but small . Once the contraction coefficients are fixed after the orbital optimization, the Hamiltonian and overlap matrices are directly constructed for the small without constructing the elements for the larger primitive orbitals, since we can directly utilize the contracted orbital as a numerical table because of the use of numerical orbitals, which is also a reason why the optimization scheme could be totally efficient.
A rather technical but important problem still remains in the application of the two step optimization method. To avoid the orbital optimization to a local minimum, we have developed the following careful procedure to provide a good initial guess for a set of coefficients :
(I) The partition of the system. A cluster is constructed including the nearest neighboring atoms for each atom .
(II) Solving of the Kohn-Sham equation of each cluster. By non self-consistently solving the Kohn-Sham equation of each cluster which is centered on an atom , we obtain the coefficients for the atom of an one-particle wave function
| (11) |
with an eigenvalue .
(III) Construction of from . Then, is given as
| (12) |
where is the Fermi function, a local chemical potential for the cluster , and N a normalization factor. For , the coefficients are generated by the Gram-Schmidt orthonormalization from and in order of the magnitude of .
To find a good initial guess for the coefficients , we tried to estimate the ratio of coefficients of the eigenstates of the whole system expanded by from the local cluster for each atom by the above treatment. Then, the eigenstates of the cluster are weighted by the Fermi function, so that the contribution of the lower states is taken into account as much as possible. Also, the contraction coefficients for are generated using the Gram-Schmidt method to avoid the overcompleteness of contracted basis orbitals. We found that the procedure provides good initial coefficients in all of our test systems, and did not observe that the orbital optimization is trapped to any serious local minimum, while the other trial was trapped to a local minimum often. The additional cost for the above procedure (I)-(III) is almost negligible, when the orbital optimization method is applied as a preconditioning of the geometry optimization as discussed later on.
3 PRIMITIVE ORBITALS
The primitive orbitals we used are eigenstates of an atomic Kohn-Sham equation with confinement pseudo potentials [8, 13]. To vanish the radial wave function of the outside of the confinement radius , we modify the atomic core potential in the all electron calculation of an atom and the generation of pseudo potential as follows:
| (13) |
where , , , and are determined, so that the value and the first derivative are continuous at both and . Figure 1 shows radial wave functions for of a carbon atom under the confinement pseudo potential. The eigenstates construct an orthonormal basis set at the same atomic position and vanish beyond within the double precision. Because of the complete vanishing tail of numerical orbitals, we find that non-zero elements of Hamiltonian and overlap matrices can be exactly proportional to the number of atoms.
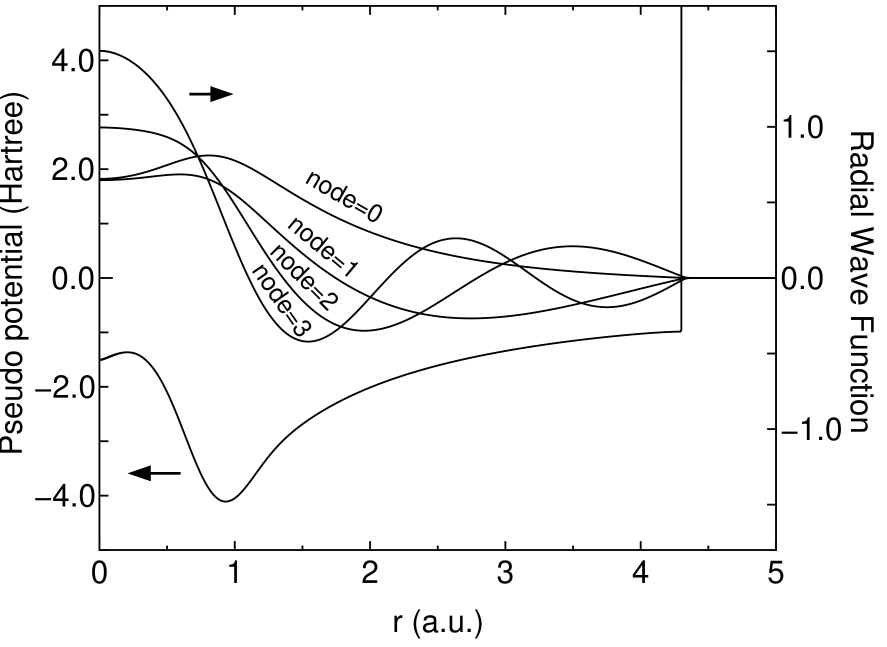
Figure 1: The radial wave function for of a carbon atom under the confinement pseudo potential obtained from Eq. (13), where 4.5 (a.u.), 4.3 (a.u.), and 3.0 (Hartree) are used for , and , respectively.
In Fig. 2 the total energy for a carbon dimer calculated using the eigenstates as a basis set is shown as a function of the number of orbitals for various cutoff radii . Factorized norm conserving pseudo potentials [13] and the local density approximation (LDA) [14] to the exchange-correlation interactions were used in our all DFT calculations. Also the real space grid techniques were used with the energy cutoff of 113 (Ryd) for numerical integrations [8]. As the cutoff radius and the number of orbitals increase, the total energy converges systematically. Thus, we see that the primitive orbitals itself are systematic basis sets controlled by two simple parameters, the cutoff radius and the number of orbitals, in the same manner as spherical wave basis sets [9]. In addition, a relatively small number of orbitals may be needed to obtain the convergent result compared to the spherical wave basis sets, since the primitive basis set is prepared for each element, unlike the spherical wave basis sets [9]. These are reasons why we use the eigenstates of an atomic Kohn-Sham equation with the confinement pseudo potentials as the primitive orbitals. A systematic study for convergence properties as a function of the cutoff radius and the number of orbitals will be presented for several elements including first row elements, alkaline metals and transition metals elsewhere.

Figure 2: The total energy for a carbon dimer calculated using the eigenstates as a basis set as a function of the number of basis orbitals per atom for the cutoff radius of 3.5, 4.0, 4.5, 5.0, 5.5 and 6.0 (a.u.).
For the later discussion, here, we introduce an abbreviation of the basis orbital as C4.5-s62p62, where C indicates the atomic symbol, 4.5 is the cutoff radius (a.u.) used in the generation, s62 means that two optimized orbitals are constructed from six primitive orbitals for the s-orbital, and the symbol signifies the restricted optimization that the radial wave function is independent on the index . In case of snn such as s66, corresponding to no optimization, snn can be simplified as sn.
4 NUMERICAL RESULTS
Figure 3 shows the convergence properties of total energies for a carbon dimer C, a methane molecule CH, and the diamond as a function of the number of unoptimized and optimized orbitals. The orbital optimization was done by five iterative steps according to Eq. (2), in which each step includes ten SCF loops. We see that the unoptimized orbitals provide systematic and rapid convergent results for not only molecules C and CH, but also a bulk system diamond, as the number of orbitals increase. Moreover, remarkable convergent results are obtained using the optimized orbitals for all systems. The small optimized orbitals rapidly converge to the total energies calculated by a larger number of unoptimized orbitals, which implies that the computational effort can be reduced significantly with a high degree of accuracy. For three systems the effect of the restriction for the orbital optimization is almost negligible, which encourages us to use the restriction, since the restricted optimization guarantees the rotational invariance of the total energy. In Fig. 4 the radial parts of the minimal orbitals obtained by the restricted optimization for the diamond are shown with those of the lowest primitive orbitals of a carbon atom for comparison. It is observed that the tails of both the optimized s- and p-orbitals shrink compared to the primitive orbitals, which clearly reveals that the basis orbital can automatically vary within the cutoff radius to minimize the total energy.
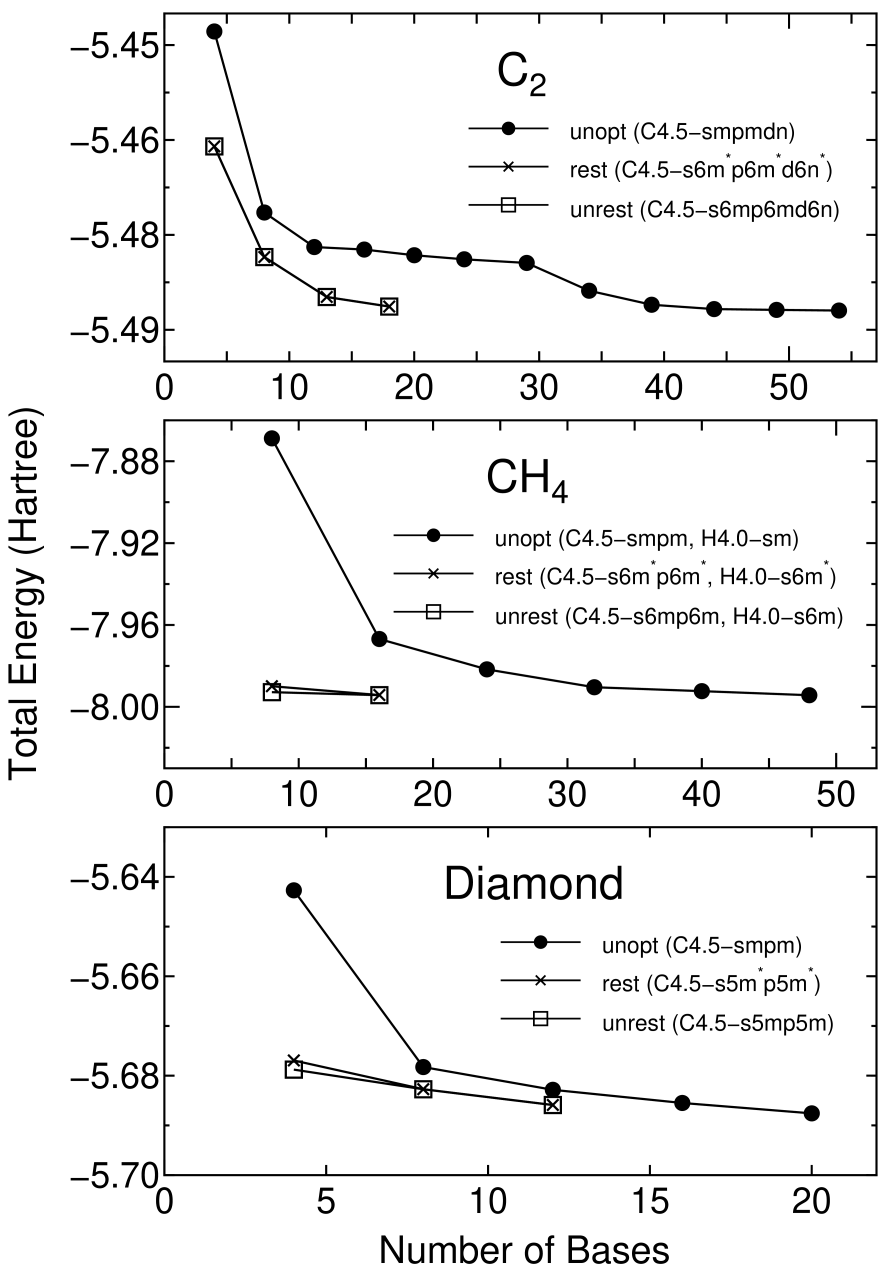
Figure 3: The total energy for a carbon dimer C, a methane CH, and the diamond as a function of the number of unoptimized (unopt) orbitals and optimized orbitals with (rest) and without (unrest) the restriction. The total energy and the number of orbitals are defined as those per atom for C and the diamond, and as those per molecule for CH. The energy cutoff of 113, 113, and 222 (Ryd) were used for the numerical integrations in C, CH, and the diamond, respectively. The two step convergence of C is due to the inclusion of d-orbitals.
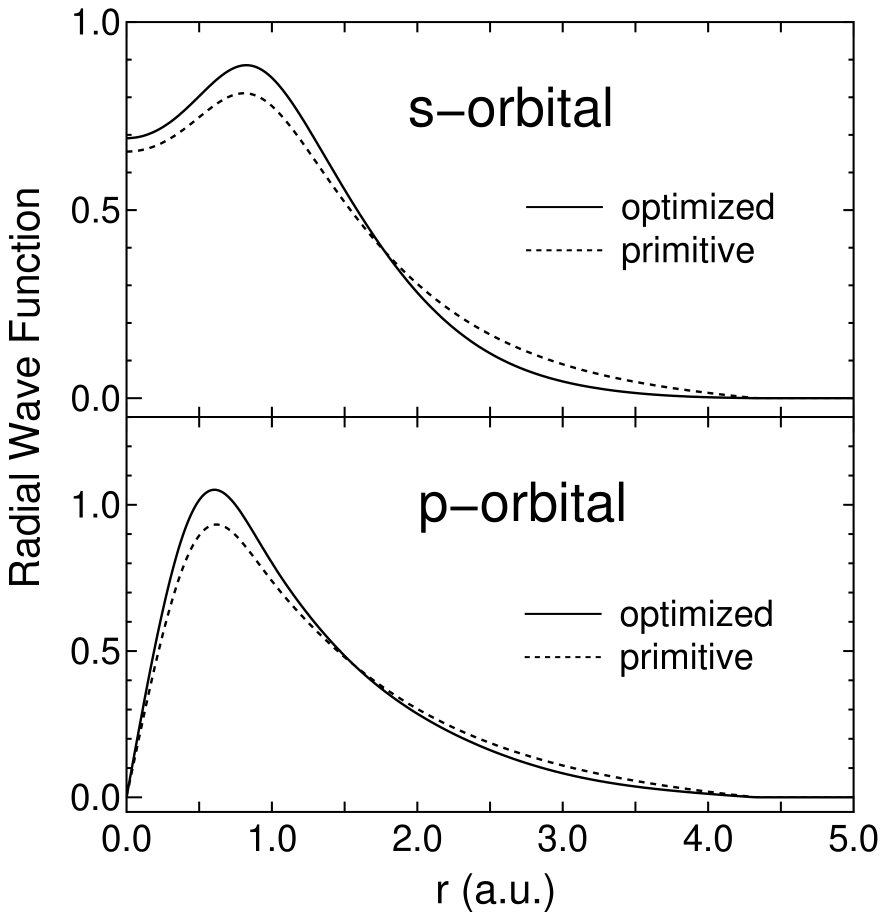
Figure 4: The radial wave function of the minimal orbitals obtained by the restricted optimization for the diamond and the lowest primitive orbitals of a carbon atom. The optimization was done in the same conditions as those in Fig. 3.
Finally, as an illustration of the orbital optimization, we performed the geometry optimization with the orbital optimization as a preconditioning for the most stable conformer of a neutral glycine molecule [15, 16] which is the smallest amino acid. Before doing the geometry optimization, the orbital optimization was performed by five iterative steps, which includes ten SCF loops per step, for an initial structure optimized by a molecular mechanics (MM). Then, the geometry optimization was done using the optimized orbitals by fifty steepest decent (SD) steps with a variable prefactor for accelerating the convergence, which includes twenty SCF loops per step. The optimized geometrical parameters are given in Table 1 together with the total energy and the computational time per MD step. In case of the unoptimized orbitals SN, TN, and TNDP, as the number of orbitals increase, we find the decrease of the total energy and the convergent geometrical parameters comparable to the experimental [16] and the other theoretical values [15]. Although there are some deviations in the optimized parameters calculated using TNDP from the other theoretical values [15], the deviations may be attributed to the pseudo potentials rather than the basis orbitals, since we verified that the optimized parameters of the glycine depend on the cutoff radii in the pseudo potential generation. Comparing to the unoptimized and optimized minimal orbitals SN and SN, it is found that the geometrical parameters are significantly improved without increasing the computational time. In case of the optimized orbitals SNP remarkable improvements are obtained in both the geometrical parameters and the computational time. The optimized orbitals SNP provide a convergent result comparable to TNDP with a great reduction of the computational time. The computational time required for the orbital optimization of SN occupies only 3 % of that of the whole calculation. So the orbital optimization can be regarded as a preconditioning before doing the geometry optimization or the molecular dynamics. Of course, it is possible to perform the orbital optimization during the geometry optimization. It is worth mentioning that the orbital optimization can be combined with an O() method [1, 2, 3, 4, 5, 6], since only and , which are calculated by the O() method, are required in Eq. (5). Therefore, the orbital optimization can be applied to large-scale systems in O() operations.
| SN | TN | TNDP | SN | SNP | Other theory | Expt. | |
| H4.0-s1 | H4.0-s3 | H4.0-s3p2 | H4.0-s31 | H4.0-s31p21 | LDA/DZP | ||
| A4.5-s1p1 | A4.5-s3p3 | A4.5-s3p3d2 | A4.5-s31p31 | A4.5-s32p31d21 | Full potential | ||
| (CC) | 1.555 | 1.535 | 1.528 | 1.515 | 1.528 | 1.510 | 1.532 |
| (NC) | 1.530 | 1.480 | 1.490 | 1.502 | 1.444 | 1.439 | 1.469 |
| (CO) | 1.353 | 1.231 | 1.235 | 1.281 | 1.238 | 1.218 | 1.207 |
| (CO) | 1.498 | 1.365 | 1.349 | 1.416 | 1.350 | 1.348 | 1.357 |
| (OH) | 1.144 | 0.998 | 0.987 | 1.010 | 0.995 | 0.988 | - |
| (NCC) | 104.8 | 106.5 | 108.2 | 108.4 | 108.8 | 114.8 | 112.1 |
| (CCO) | 136.8 | 127.9 | 128.3 | 128.9 | 125.9 | 124.9 | 125.1 |
| (COH) | 96.8 | 107.9 | 105.7 | 105.8 | 106.8 | 105.6 | - |
| C=ON | 3.132 | 2.998 | 2.905 | 2.998 | 2.882 | 2.827 | - |
| Energy (Hartree) | -55.662 | -55.981 | -56.106 | -55.818 | -56.036 | - | - |
| Time(s)/MD step | 32 | 86 | 217 | 34 | 84 | - | - |
5 CONCLUSIONS
To conclude, we have developed a simple and practical method based on the force theorem for variationally optimizing numerical atomic orbitals used in density functional calculations. The optimization algorithm similar to the geometry optimization allows us to fully optimize atomic orbitals within a cutoff radius for each atom in a given system. The illustration of geometry optimization with the orbital optimization for a small molecule clearly shows that the small optimized orbitals promise to greatly reduce the computational effort with a high degree of accuracy.
ACKNOWLEDGMENTS
We would like to thank H. Kino for helpful suggestions and discussions. This work was partly supported by NEDO under the Nanotechnology Materials Program.
References
- [1] W. Yang, Phys. Rev. Lett. 66, 1438 (1991).
- [2] S. Goedecker and L. Colombo, Phys. Rev. Lett. 73, 122 (1994).
- [3] G. Galli and M. Parrinello, Phys. Rev. Lett. 69, 3547 (1992).
- [4] X.-P. Li, R. W. Nunes, and D. Vanderbilt, Phys. Rev. B 47, 10891 (1993); M. S. Daw, Phys. Rev. B 47, 10895 (1993).
- [5] T. Ozaki and K. Terakura, Phys. Rev. B 64, 195126 (2001).
- [6] S. Goedecker, Rev. of Mod. Phys. 71, 1085 (1999) and references therein.
- [7] S. D. Kenny, A. P. Horsfield, and H. Fujitani, Phys. Rev. B 62, 4899 (2000).
- [8] J. Junquera, . Paz, D. Snchez-Portal, and E. Artacho, Phys. Rev. B 64, 235111 (2001); J. M. Soler et al., J. Phys.:Condens. Matter 14, 2745 (2002) and references therein.
- [9] C. K. Gan, P. D. Haynes, and M. C. Payne, Phys. Rev. B 63, 205109 (2001).
- [10] J. D. Talman, Phys. Rev. Lett. 84, 855 (2000).
- [11] R. Car and M. Parrinello, Phys. Rev. Lett. 55, 2471 (1985).
- [12] M. C. Payne, M. P. Teter, D. C. Allan, T. A. Arias and J. D. Joannopoulos, Rev. Mod. Phys. 64, 1045(1992) and references therein.
- [13] G. B. Bachelet, D. R. Hamann, and M. Schlter, Phys. Rev. B 26, 4199 (1982); L. Kleinman and D. M. Bylander, Phys. Rev. Lett. 48, 1425 (1982).
- [14] J. P. Perdew and A. Zunger, Phys. Rev. B 23, 5048 (1981).
- [15] V. Barone, C. Adamo, and F. Lelj, J. Chem. Phys. 102, 364 (1995).
- [16] K. Iijima, K. Tanaka, and S. Onuma, J. Mol. Struct. 246, 257 (1991).