Numerical Evaluation of Electron Repulsion Integrals for
Pseudo-Atomic Orbitals and Their Derivatives
Masayuki Toyoda and Taisuke Ozaki
and Taisuke Ozaki
Research Center for Integrated Science,
Japan Advanced Institute of Science and Technology,
1-1, Asahidai, Nomi, Ishikawa 932-1292, Japan
Copyright 2009 American Institute of Physics.
This article is provided by the author for the reader's personal use only.
Any other use requires prior permission of the author and the American Institute of Physics.
The following article appeared in Journal of Chemical Physics 130, 124114 (2009)
and may be found at
http://link.aip.org/link/?JCPSA6/130/124114/1.
NOTICE: This is the authorfs version of a work accepted for publication by American Institute of Physics.
Changes resulting from the publishing process, including peer review, editing,
corrections, structural formatting and other quality control mechanisms, may
not be reflected in this document. Changes may have been made to this work
since it was submitted for publication.
Abstract
A numerical method to calculate the four-center
electron-repulsion integrals for strictly localized
pseudo-atomic orbital basis sets has been developed.
Compared to the conventional Gaussian expansion method,
this method has an advantage in ease of combination
with 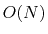 density functional calculations.
Additional mathematical derivations are also presented
including the analytic derivatives of the integrals with
respect to atomic positions and spatial damping
of the Coulomb interaction due to the screening effect.
In the numerical test for a simple molecule, the convergence
up to
density functional calculations.
Additional mathematical derivations are also presented
including the analytic derivatives of the integrals with
respect to atomic positions and spatial damping
of the Coulomb interaction due to the screening effect.
In the numerical test for a simple molecule, the convergence
up to 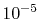 Hartree in energy is successfully
obtained with a feasible cost of computation.
Hartree in energy is successfully
obtained with a feasible cost of computation.
Introduction
In ab initio electronic structure calculations based on the
density-functional theory (DFT), the Fock exchange for Kohn-Sham
orbitals has been occasionally used as the ``exact'' exchange
in order to improve the poor description of exchange energy by
the Dirac exchange which is the standard functional used in the
local density approximation (LDA) and the generalized gradient
corrections (GGA).
In recent years, various molecular systems have been calculated
by using the hybrid functional methods [1], such as
B3LYP [2,3] and PBE0 [4],
where a certain amount of the Fock exchange is admixed with the
LDA/GGA exchange-correlation functionals.
The introduction of the non-local Fock exchange significantly
improves the delocalization error [5] in the
semi-local LDA/GGA functional and presents better thermochemical
and structural properties of molecules.
The heavy computational demand to evaluate the Fock exchange is,
however, a serious drawback.
The studies for large molecules and solids are thus very limited.
One solution for this problem is given in the
Heyd-Scuseria-Ernzerhof (HSE) hybrid functional [6]
where the long tail of the Coulomb interaction is somewhat
artificially damped.
The successful application of the HSE hybrid functional to extended
systems, typified by the surprisingly accurate values of the
band-gap energies of semiconductors [7], implies that
the damping scheme they introduced is not just conducive to
reducing the computational cost, but reasonable as well to describe
the screening of the Coulomb interaction in real materials.
The Fock exchange consists of the four-center electron
repulsion integrals (ERI) among basis functions.
Since the integration can be performed analytically
with the Gaussian-type orbital (GTO) basis functions,
the Gaussian-expansion method is conventionally used
in the evaluation of ERI where the basis functions
are expanded in terms of GTO basis set
[8,9,10].
However, the Gauss transform of a numerically defined
function might require an indirect way such as a
fitting process of the function to analytic functions
unlike that for the Slater-type orbital (STO)
functions [8].
While, in our method, ERI is evaluated directly from
arbitrarily defined basis functions.
Specifically in the 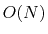 DFT calculation codes, such as
CONQUEST [11], SIESTA [12]
and OpenMX [13,14,15], the strictly
localized pseudo-atomic orbital (PAO) basis sets are commonly
used since the real space sparsity of the resultant Hamiltonian
and overlap matrices enables us to combine the scheme with
various
DFT calculation codes, such as
CONQUEST [11], SIESTA [12]
and OpenMX [13,14,15], the strictly
localized pseudo-atomic orbital (PAO) basis sets are commonly
used since the real space sparsity of the resultant Hamiltonian
and overlap matrices enables us to combine the scheme with
various 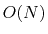 methods and to parallelize the computation by the
domain decomposition in real space.
Therefore, toward the implementation of the hybrid functionals
or any other methods which utilizes the Fock exchange in the
methods and to parallelize the computation by the
domain decomposition in real space.
Therefore, toward the implementation of the hybrid functionals
or any other methods which utilizes the Fock exchange in the
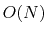 DFT calculations, an effective numerical method is
required to evaluate the Fock exchange with using the non-analytic
PAO basis functions.
DFT calculations, an effective numerical method is
required to evaluate the Fock exchange with using the non-analytic
PAO basis functions.
In this paper, we present a numerical procedure to calculate the
four-center ERI for the numerically defined basis functions.
We briefly review the mathematical derivations in the next section.
Then, based on the formulations, we derive the analytic derivatives
of the integrals with respect to atomic positions, which are
required for the calculation of the forces on atoms.
Our derivation is fully analytic and consistent with the integrals
themselves.
We also derive the formulation of ERI when the spatial damping
of the Coulomb interaction is introduced as in the HSE
hybrid functional.
Numerical evaluation of ERI
The essential mathematical analysis described in this section
is provided by Talman [16].
The considered wavefunctions are expressed as the
linear combination of the PAO basis functions (LCPAO)
and each basis function is a product of a numerically defined
radial function 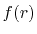 and an eigenfunction of angular momentum
i.e. the spherical harmonic function
and an eigenfunction of angular momentum
i.e. the spherical harmonic function
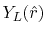 for given angular momentum
for given angular momentum
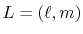 :
:
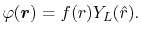 |
(1) |
The Fock exchange for the wavefunctions is then expressed as
the sum of ERI for the basis functions.
In general, ERI for four basis functions centered at
different positions 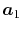 ,
, 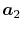 ,
, 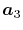 and
and
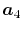 is defined as follows:
is defined as follows:
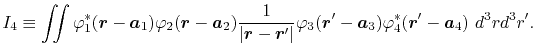 |
(2) |
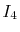 is also denoted as
is also denoted as
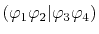 to make the
order of the basis functions clear.
This integral is quite difficult to compute since the integration has
to be performed over six-dimensional space coordinates.
To reduce the dimensionality of the coordinates, one first needs
to describe the overlap of the basis functions
to make the
order of the basis functions clear.
This integral is quite difficult to compute since the integration has
to be performed over six-dimensional space coordinates.
To reduce the dimensionality of the coordinates, one first needs
to describe the overlap of the basis functions 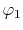 and
and
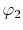 as a function centered at an arbitrarily chosen center
as a function centered at an arbitrarily chosen center
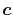 which will be referred to as the overlap function later,
and, similarly, the overlap of
which will be referred to as the overlap function later,
and, similarly, the overlap of 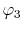 and
and 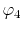 at another center
at another center 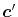 ,
,
Then, the integral Eq. (2) becomes
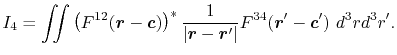 |
(5) |
By using the Fourier transform of the Coulomb interaction 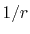 ,
,
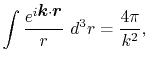 |
(6) |
the integral in reciprocal space is expressed as a single-center
integral,
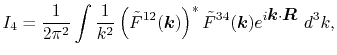 |
(7) |
where
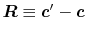 and
and
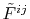 are
the Fourier transformed functions of Eqs. (3)
and (4).
Since
are
the Fourier transformed functions of Eqs. (3)
and (4).
Since
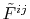 are also expanded
in terms of the spherical harmonic functions,
are also expanded
in terms of the spherical harmonic functions,
the angular part of the integral in Eq. (7)
can be performed analytically, where the overlap coefficient,
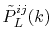 , is a radial function of
, is a radial function of 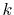 which will be
discussed later on.
Finally, the integral Eq. (2) is broken down
to a sum of single-dimensional integrals as follows:
which will be
discussed later on.
Finally, the integral Eq. (2) is broken down
to a sum of single-dimensional integrals as follows:
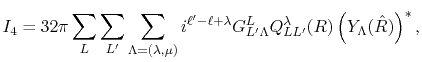 |
(9) |
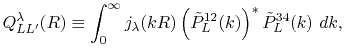 |
(10) |
where
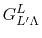 is the Gaunt coefficients defined by
is the Gaunt coefficients defined by
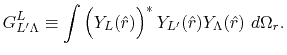 |
(11) |
The remaining problem is how to calculate
the overlap coefficients
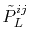 in
Eq. (8).
In order to calculate them, the translation of expansion
center of a basis function is considered based on the investigation
by Löwdin [17] as follows:
in
Eq. (8).
In order to calculate them, the translation of expansion
center of a basis function is considered based on the investigation
by Löwdin [17] as follows:
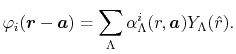 |
(12) |
The coefficients
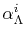 , often referred to as
, often referred to as
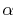 -function, are given by
-function, are given by
with a function of 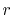 and
and 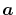 defined by
defined by
Here,
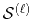 is the
is the 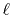 -th order spherical Bessel
transform and
-th order spherical Bessel
transform and
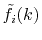 is the transformed radial function
given by
is the transformed radial function
given by
The overlap functions, Eqs. (3) and
(4), are described
in terms of 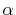 -functions Eq. (13):
-functions Eq. (13):
where
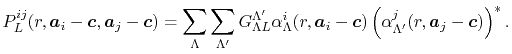 |
(17) |
Finally, by transforming Eq. (17),
the overlap coefficients in reciprocal space are obtained as
![$\displaystyle {\tilde P}^{ij}_L(k) = {\cal S}^{(\ell)} \left[ \vphantom{\sum} P^{ij}_L(r, \vec a_i - \vec c, \vec a_j - \vec c) \right] .$](img70.png) |
(18) |
Let us summarize how to compute ERI in the present approach:
The first step is to transform the radial part of
the basis functions by Eq. (15).
Then, for every pair of orbitals, 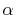 -functions
are calculated through Eqs. (13) and (14).
From those
-functions
are calculated through Eqs. (13) and (14).
From those 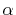 -functions, the overlap coefficients
Eq. (17) and the transformed ones
Eq. (18) are obtained.
Finally, the integral Eq. (9) is calculated by summing
up the radial integrals Eq. (10).
-functions, the overlap coefficients
Eq. (17) and the transformed ones
Eq. (18) are obtained.
Finally, the integral Eq. (9) is calculated by summing
up the radial integrals Eq. (10).
Fast Spherical Bessel transform
In the above approach, the spherical Bessel
transform (SBT) is performed at three different
places, namely, Eqs. (14),
(15) and (18).
Since the orders of the transforms are different and high
at each step, this process can be a source of numerical errors
as well as a bottleneck in the computation speed.
A careful examination is therefore required in
implementing the numerical method of SBT.
In the preceding works by Talman, the fast spherical Bessel
transform technique is used, which is proposed by
Siegman [18] and Talman [19].
In our experience of testing several numerical techniques,
such as the discrete Bessel transform [20]
and the asymptotic expansion method [21],
we have reached the conclusion that the Siegman-Talman's
fast SBT method is actually the most stable and fast for
the present approach [22].
It, however, still suffers from oscillating numerical error
in high-order transforms.
The error becomes more significant for the PAO basis functions than
the analytic basis functions because of their finite truncation.
Fortunately, the oscillating error can be substantially suppressed
by applying a simple correction to the fast SBT method
as we describe later in this section.
In the fast SBT method, the radial variables 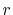 and
and 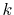 are changed
to their logarithms,
are changed
to their logarithms,
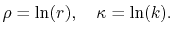 |
(19) |
Then SBT of a function 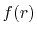 with order
with order 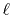 ,
,
![$\displaystyle {\tilde f}(k) = {\cal S}^{(\ell)} \left[ \vphantom{\sum} f(r) \right] \equiv \int_0^\infty j_\ell(kr) f(r) r^2 \ dr ,$](img78.png) |
(20) |
becomes a convolution-type integral as follows:
where
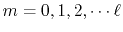 is an arbitrarily chosen parameter
and
is an arbitrarily chosen parameter
and 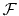 is the Fourier transform.
is the Fourier transform.
The function
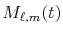 is the Fourier transformed
spherical Bessel function:
is the Fourier transformed
spherical Bessel function:
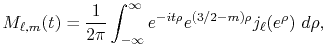 |
(22) |
where the integral can be performed analytically [19].
The transform, Eq. (21), is thus reduced to a couple
of consecutive one-dimensional Fourier transforms, where we can
take advantages of the speed of the fast Fourier transform (FFT)
algorithm.
As mentioned before, the fast SBT method suffers from the
oscillating numerical error in high-order transforms.
In Fig. 1, a typical example of such error is shown,
where a PAO basis function is transformed with the order 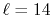 and
and 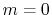 , and then back-transformed with the same order.
In the transformed function (the upper middle panel), the oscillating
error appears in the small-
, and then back-transformed with the same order.
In the transformed function (the upper middle panel), the oscillating
error appears in the small-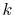 region.
After the back-and-forth transform (the upper right-hand panel), the
accumulation of error is observed.
Often, the error approaches quickly to infinity and the computation
crashes.
region.
After the back-and-forth transform (the upper right-hand panel), the
accumulation of error is observed.
Often, the error approaches quickly to infinity and the computation
crashes.
In order to avoid the error, a simple correction is applied.
Since the error appears only in the small-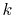 region, we perform the
integration of Eq. (20) for some selected
region, we perform the
integration of Eq. (20) for some selected 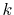 -points
between 0 and
-points
between 0 and 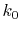 by using the straightforward trapezoidal method,
where
by using the straightforward trapezoidal method,
where 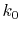 is smaller than the smallest
is smaller than the smallest 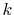 -points used in the
final integration Eq. (10) so that the effect of the
correction can be negligible, but the numerical breakdown can be
avoided.
By a linear interpolation between the selected
-points used in the
final integration Eq. (10) so that the effect of the
correction can be negligible, but the numerical breakdown can be
avoided.
By a linear interpolation between the selected 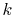 -points,
we obtain another transformed function
-points,
we obtain another transformed function
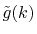 ,
in addition to
,
in addition to
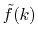 .
Then we replace
.
Then we replace
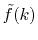 with
with
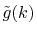 for
for 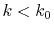 as follows:
as follows:
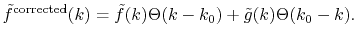 |
(23) |
This rather crude way of correction actually serves for the practical
purpose.
The lower panels of Fig. 1 show the example of the
back-and-forth transform of the PAO basis function with
the corrected fast SBT.
Here, we use
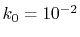 and the straightforward integration
are performed only for three selected
and the straightforward integration
are performed only for three selected 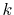 -points which are
-points which are 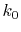 ,
,
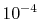 and 0.
It is confirmed that the oscillating error is successfully suppressed.
and 0.
It is confirmed that the oscillating error is successfully suppressed.
Figure 1:
Accumulation of numerical error by back-and-forth
transforms with the fast SBT method.
The input function (a) is a PAO orbital
of H atom for 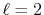 and
and
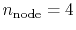 .
The transformed function of (a) is plotted in the
panel (b), and the back-transformed of (b) in the
panel (c).
In the lower panels (d), (e) and (f), accumulation of
numerical error by back-and-forth
transforms with our modified fast SBT method is shown,
where the error is substantially suppressed.
.
The transformed function of (a) is plotted in the
panel (b), and the back-transformed of (b) in the
panel (c).
In the lower panels (d), (e) and (f), accumulation of
numerical error by back-and-forth
transforms with our modified fast SBT method is shown,
where the error is substantially suppressed.
|
Derivatives
For the calculation of forces acting on atoms, we derive the
derivatives of the integral Eq. (9) with respect
to atomic positions.
In our derivation, the expansion centers for the overlap functions
are assumed to be given by the following forms:
where
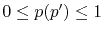 .
Having in mind that
.
Having in mind that
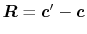 , the derivatives
are obtained as
, the derivatives
are obtained as
where the vectors 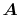 ,
,
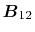 and
and
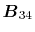 are defined as
are defined as
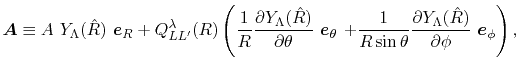 |
(30) |
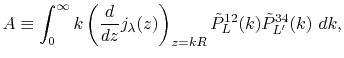 |
(31) |
Here, the unit vectors are defined as follows:
where 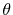 and
and 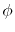 are the spherical coordinate components
of the vector
are the spherical coordinate components
of the vector 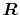 .
.
The vector 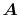 can be calculated immediately since
all the differentiations in Eqs. (30) and (31)
are taken for the analytic functions.
As shown in the appendix, the differentiations of the
overlap functions in Eqs. (32) and (33) can also be performed completely analytically.
Note that the differentiations are taken only for
can be calculated immediately since
all the differentiations in Eqs. (30) and (31)
are taken for the analytic functions.
As shown in the appendix, the differentiations of the
overlap functions in Eqs. (32) and (33) can also be performed completely analytically.
Note that the differentiations are taken only for 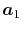 and
and
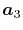 because the others can also be obtained via the
following sum rule:
because the others can also be obtained via the
following sum rule:
The rule arises due to the assumption of Eqs. (24)
and (25), and this is the reason why we have assumed them.
There is another sum rule:
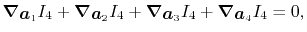 |
(39) |
which is a more general one arising from the definition
of the integral.
It is easily confirmed that the derivatives Eqs. (26),
(27), (28) and (29) satisfy the rule.
Screening of the Coulomb interaction
We also derive the formulation of ERI when the screening of
Coulomb interaction is introduced.
The screening scheme is assumed to be the same with that used
in the HSE hybrid functional [6],
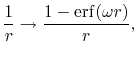 |
(40) |
where
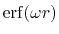 is the Gauss error function and
is the Gauss error function and 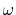 is a screening parameter.
The Fourier transform of the screened Coulomb interaction is
is a screening parameter.
The Fourier transform of the screened Coulomb interaction is
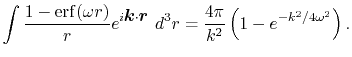 |
(41) |
Therefore, the radial integral Eq. (10) becomes
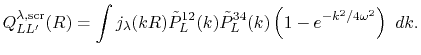 |
(42) |
Since the screening factor is independent of the atomic positions,
the derivatives are still in the similar forms as Eqs. (26),
(27), (28) and (29).
Except, the radial integrals Eqs. (31),
(32) and (33) are replaced with the screened ones
as follows:
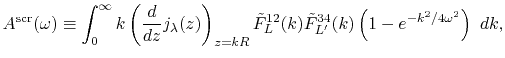 |
(43) |
Computation speed
Our motivation is in the application of the Fock exchange
in large systems such as large molecules and solids.
In those systems, an enormous (infinite for
solids) number of combinations of basis functions
have to be considered.
Fortunately for the PAO basis sets, since they are strictly
confined in real space, the overlaps are exactly zero whenever
the distance between the basis functions is longer than the
sum of the confinement lengths.
On the other hand, however, any two overlap functions can
interact with each other even if they are separated quite
far apart because of the infinitely long tail of the Coulomb
interaction.
By using the screening scheme described in the previous
section, it might be justified to neglect the contribution
from the far-separated pairs.
Nevertheless, still a large number of pairs have to be
calculated since the typical value of the screening parameter is
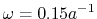 and thus the effective screening
length is
and thus the effective screening
length is
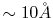 [7].
Therefore, we should consider to make the computation
faster for the final integration Eqs. (9) and
(10).
As already pointed out by Talman, the
convergence of the summation Eq. (9) is very fast
so that the cutoff angular momentum
[7].
Therefore, we should consider to make the computation
faster for the final integration Eqs. (9) and
(10).
As already pointed out by Talman, the
convergence of the summation Eq. (9) is very fast
so that the cutoff angular momentum
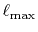 and the
number of
and the
number of 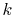 -sampling points
-sampling points 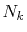 can be decreased.
We shall define new parameters
can be decreased.
We shall define new parameters
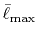 and
and
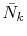 for Eqs. (9) and (10)
in order to distinguish from the original parameters
for Eqs. (9) and (10)
in order to distinguish from the original parameters
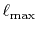 and
and 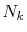 which are used in the other parts.
Typically,
which are used in the other parts.
Typically,
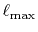 has to be as large as
has to be as large as 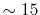 to describe the overlap functions accurately.
While, as shown later,
to describe the overlap functions accurately.
While, as shown later,
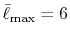 is
enough to obtain
is
enough to obtain 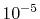 Hartree accuracy in energy even when
Hartree accuracy in energy even when 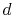 orbitals are involved.
Similarly,
orbitals are involved.
Similarly, 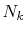 is required to be
is required to be 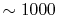 , while, in the
final integration, the Gauss-Laguerre quadrature can be used
which gives good convergence with
, while, in the
final integration, the Gauss-Laguerre quadrature can be used
which gives good convergence with
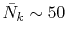 .
.
The location of the expansion centers 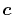 has also
a significant effect on the convergence speed.
In general,
has also
a significant effect on the convergence speed.
In general, 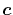 is an orbital-dependent value.
Therefore, since
is an orbital-dependent value.
Therefore, since 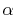 -functions Eqs. (13)
and (14) depend on
-functions Eqs. (13)
and (14) depend on 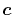 (note that what we
actually need is the terms in the right-hand side of Eq.
(17)), one needs to calculate those coefficients
of which the number is equivalent to that of neighboring orbitals.
Here, we offer a suggestion that the computation cost may be
reduced by choosing
(note that what we
actually need is the terms in the right-hand side of Eq.
(17)), one needs to calculate those coefficients
of which the number is equivalent to that of neighboring orbitals.
Here, we offer a suggestion that the computation cost may be
reduced by choosing 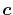 at the middle of the two orbital centers,
at the middle of the two orbital centers,
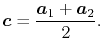 |
(46) |
In this case, the required number of 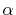 -functions
is decreased by a factor of the number of orbitals per atom, which is
typically
-functions
is decreased by a factor of the number of orbitals per atom, which is
typically 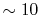 .
Note that Eq. (46) is not the best choice if
just one ERI is considered.
In fact, the choice of of
.
Note that Eq. (46) is not the best choice if
just one ERI is considered.
In fact, the choice of of 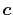 with considering the
spatial extent of each orbital gives faster convergence
in the final integration [23].
Therefore, it becomes a competition between the convergence speed
in performing a single integral and the required number of
with considering the
spatial extent of each orbital gives faster convergence
in the final integration [23].
Therefore, it becomes a competition between the convergence speed
in performing a single integral and the required number of
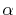 -functions.
-functions.
Computation results
In order to check the convergence properties of our routine,
we first performed calculations of ERI for a GTO basis set.
Three different integrals 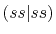 ,
, 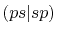 and
and 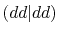 are calculated.
The definition of the basis functions for the integrals is
listed in Table 1.
For all the integrals, the orbital locations are fixed to the
corners of a square on the
are calculated.
The definition of the basis functions for the integrals is
listed in Table 1.
For all the integrals, the orbital locations are fixed to the
corners of a square on the 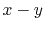 plane with edge length of 1;
plane with edge length of 1;
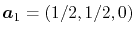 ,
,
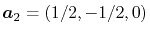 ,
,
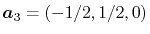 and
and
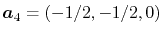 .
The cutoff for the angular momentum is
.
The cutoff for the angular momentum is
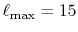 and the number of radial mesh points is
and the number of radial mesh points is 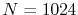 .
In the final integration, the Gauss-Laguerre quadrature is used
where the number of k-sampling points is
.
In the final integration, the Gauss-Laguerre quadrature is used
where the number of k-sampling points is
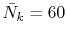 and
the summation is taken up to a reduced cutoff
and
the summation is taken up to a reduced cutoff
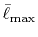 .
In Table 2, the calculated values of the integrals are
shown for increasing
.
In Table 2, the calculated values of the integrals are
shown for increasing
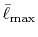 , where they are left blank
after the convergence up to
, where they are left blank
after the convergence up to 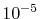 Hartree is achieved.
The exact values are also shown for comparison, which are
obtained by using the analysis given in literature [9].
It is clearly found that the convergence becomes slower for orbitals
with higher angular momentum.
Nevertheless, the accurate values for all the
integrals up to
Hartree is achieved.
The exact values are also shown for comparison, which are
obtained by using the analysis given in literature [9].
It is clearly found that the convergence becomes slower for orbitals
with higher angular momentum.
Nevertheless, the accurate values for all the
integrals up to 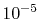 Hartree are obtained with
Hartree are obtained with
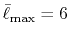 .
.
Table:
Definition of the integrals in the calculations of ERI for GTO.
| integral |
function |
radial |
angular |
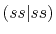 |
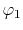 , , 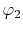 , , 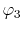 , , 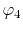 |
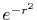 |
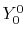 |
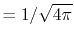 |
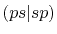 |
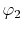 , , 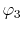 |
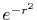 |
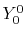 |
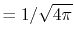 |
| |
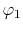 |
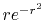 |
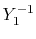 |
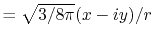 |
| |
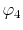 |
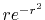 |
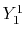 |
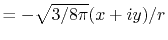 |
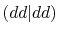 |
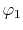 |
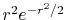 |
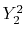 |
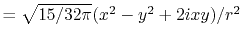 |
| |
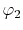 |
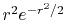 |
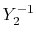 |
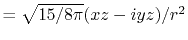 |
| |
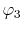 |
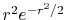 |
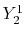 |
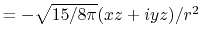 |
| |
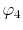 |
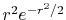 |
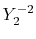 |
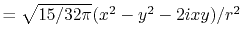 |
|
Table:
Convergence of the calculations of ERI for
GTO basis set with respect to the cutoff parameter
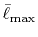 .
.
| |
Integrals (Hartree) |
 |
 |
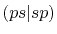 |
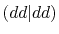 |
| 0 |
0.007608 |
0.002853 |
0.000000 |
| 1 |
|
0.002384 |
0.001055 |
| 2 |
|
0.002512 |
0.000305 |
| 3 |
|
|
0.002656 |
| 4 |
|
|
-0.001909 |
| 5 |
|
|
-0.001909 |
| 6 |
|
|
-0.001965 |
| exact |
0.007608 |
0.002512 |
-0.001966 |
|
As a more realistic example, we performed calculations of ERI
of a methane molecule for a Slater-type orbital (STO) basis set.
The basis functions and the atomic positions are summarized in
Table 3.
Our results and the comparison values which are calculated
by using the Gaussian expansion method [9] are
shown in Table 4.
For all the integrals considered, ours and the comparison
values agree with each other up to 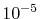 Hartree.
The difference from the comparison values is large for
Hartree.
The difference from the comparison values is large for 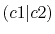 and
and
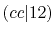 because the C-
because the C-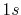 inner-shell orbital is involved.
In general, the small spatial extent of such the inner-shell orbitals
makes the convergence slower.
This, however, would not have to be considered so seriously in the
actual calculations if the contribution of the inner-shell
electrons are included in the pseudopotentials.
inner-shell orbital is involved.
In general, the small spatial extent of such the inner-shell orbitals
makes the convergence slower.
This, however, would not have to be considered so seriously in the
actual calculations if the contribution of the inner-shell
electrons are included in the pseudopotentials.
Table:
Basis functions and atomic positions in the calculations of methane molecule.
The STO basis functions are normalized.
| Symbol |
Atom |
Orbital |
Position |
Exponent |
| |
|
|
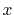 |
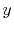 |
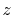 |
|
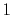 |
H |
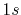 |
0 |
0 |
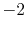 |
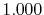 |
 |
H |
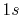 |
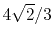 |
0 |
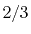 |
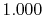 |
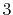 |
H |
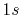 |
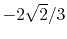 |
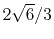 |
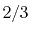 |
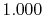 |
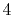 |
H |
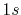 |
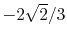 |
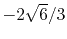 |
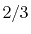 |
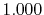 |
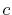 |
C |
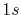 |
0 |
0 |
0 |
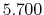 |
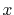 |
C |
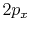 |
0 |
0 |
0 |
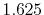 |
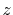 |
C |
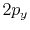 |
0 |
0 |
0 |
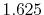 |
|
Table:
Convergence of the calculations of ERI of methane
molecule for the STO basis set.
The symbols 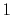 ,
, 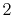 ,
, 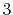 ,
, 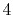 ,
, 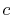 ,
, 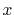 and
and 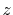 specify the STO basis functions of H and C atoms.
See Table 3 for details.
The comparison values are taken from ref. [9].
specify the STO basis functions of H and C atoms.
See Table 3 for details.
The comparison values are taken from ref. [9].
| |
Integrals (Hartree) |
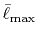 |
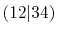 |
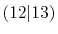 |
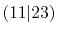 |
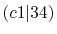 |
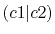 |
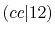 |
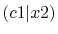 |
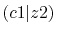 |
| 0 |
0.031420 |
0.035743 |
0.097301 |
0.013109 |
0.011258 |
0.170321 |
0.026924 |
0.009519 |
| 1 |
0.031420 |
0.035743 |
0.097301 |
0.013010 |
0.011186 |
0.170321 |
0.020083 |
0.006288 |
| 2 |
0.030647 |
0.035666 |
0.095631 |
0.012719 |
0.011188 |
0.166242 |
0.020144 |
0.006106 |
| 3 |
0.030647 |
0.035666 |
0.095631 |
0.012723 |
0.011188 |
0.166242 |
0.019819 |
0.005914 |
| 4 |
0.030684 |
0.035694 |
0.095709 |
0.012743 |
0.011188 |
0.166578 |
0.019834 |
0.005902 |
| 5 |
0.030684 |
0.035694 |
0.095709 |
0.012743 |
0.011188 |
0.166578 |
0.019809 |
0.005887 |
| 6 |
0.030681 |
0.035694 |
0.095703 |
0.012741 |
0.011188 |
0.166531 |
0.019811 |
0.005887 |
| comp. |
0.030683 |
0.035694 |
0.095706 |
0.012741 |
0.011195 |
0.166536 |
0.019809 |
0.005885 |
|
Calculations of ERI for a PAO basis set are performed for the
methane structure.
The PAO data is taken from those used in OpenMX DFT calculation
package [24].
The ground state orbitals generated by the confinement scheme
[13] with the radius of 5.0 Bohr are used as the
PAO basis functions for both the hydrogen and carbon atoms.
The calculated values are shown in Table 5 where
the parameters
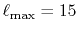 ,
, 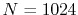 and
and
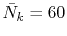 are used.
The comparison values are also calculated by using the present
method with the enhanced parameters
are used.
The comparison values are also calculated by using the present
method with the enhanced parameters
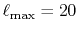 and
and 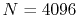 .
As well as the analytic functions such as GTO and STO basis sets,
even for the strictly localized PAO basis set, it is confirmed that
the convergence up to
.
As well as the analytic functions such as GTO and STO basis sets,
even for the strictly localized PAO basis set, it is confirmed that
the convergence up to 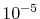 Hartree is obtained with
Hartree is obtained with
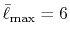 .
.
Table:
Convergence of the calculations of ERI of methane molecule
for the PAO basis set.
The symbols and the atomic positions are the same as in Table
3.
The comparison values are also calculated by using the present
method with enhanced parameters (see text for details).
| |
Integrals (Hartree) |
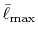 |
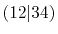 |
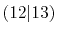 |
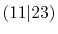 |
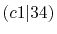 |
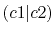 |
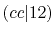 |
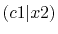 |
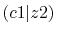 |
| 0 |
0.031071 |
0.035881 |
0.096122 |
0.070962 |
0.158759 |
0.141194 |
-0.044336 |
0.047671 |
| 1 |
0.031071 |
0.035881 |
0.096122 |
0.071814 |
0.161936 |
0.141194 |
-0.030393 |
0.018107 |
| 2 |
0.030601 |
0.035835 |
0.095266 |
0.071497 |
0.162871 |
0.140576 |
-0.031044 |
0.020152 |
| 3 |
0.030601 |
0.035835 |
0.095266 |
0.071508 |
0.162823 |
0.140576 |
-0.030911 |
0.019802 |
| 4 |
0.030630 |
0.035860 |
0.095316 |
0.071517 |
0.162851 |
0.140577 |
-0.030915 |
0.019825 |
| 5 |
0.030630 |
0.035860 |
0.095316 |
0.071517 |
0.162851 |
0.140577 |
-0.030906 |
0.019826 |
| 6 |
0.030627 |
0.035860 |
0.095313 |
0.071516 |
0.162855 |
0.140577 |
-0.030905 |
0.019828 |
| comp. |
0.030630 |
0.035862 |
0.095318 |
0.071519 |
0.162859 |
0.140581 |
-0.030903 |
0.019829 |
|
The computation time in our method for calculating
a single integral is 3.0 sec with Intel Xeon processor
3.2 GHz.
This is too expensive compared to the time required in
the conventional Gaussian-expansion method, e.g.,
one of the most sophisticated program takes only
0.5 - 1.3 msec per integral with Intel Pentium IV
processor 3.2 GHz [10].
In our method, the most of the time is consumed in
the calculation of the overlap functions.
Fortunately, the required number of pairs is
proportional to the number of the basis functions
due to the finite truncation of the PAO basis functions,
whereas the effort of the computation of ERIs scales
quadratically as the number of the basis functions
increases.
In addition to that, the overlap functions can be
reused for the calculations of ERI with a different
pair of them, e.g., the overlap of 1 and 2 for
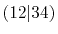 can also be used for
can also be used for 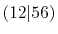 etc.
Therefore, the computation efficiency in total can
be significantly enhanced as the system size becomes
larger.
etc.
Therefore, the computation efficiency in total can
be significantly enhanced as the system size becomes
larger.
Summary
In summary, a numerical method to evaluate ERI for the PAO basis
sets has been developed.
Based on the mathematical analysis by Talman, we derive
the analytic derivatives and a spatial damping scheme for
the Coulomb interaction.
We also propose a numerical method for SBT of the strictly
localized PAO basis functions,
where the oscillating numerical error is well suppressed
even for the high-order transforms.
In the numerical calculations for a simple molecule,
the convergence up to 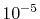 Hartree in energy has been
successfully obtained.
The present method enables us to utilize state-of-the-art
hybrid functional methods in the
Hartree in energy has been
successfully obtained.
The present method enables us to utilize state-of-the-art
hybrid functional methods in the 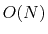 DFT calculation
programs.
DFT calculation
programs.
Acknowledgments
This work was partly supported by CREST-JST and the
Next Generation Super Computing Project, Nanoscience Program,
MEXT, Japan.
addtoresetequationsection
Appendix
The derivatives of the overlap functions in the vectors
Eqs. (32) and (33) are given as
where we use the assumption in Eqs. (24)
and (25).
Then, the derivatives of the 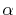 -functions are
-functions are
where the unit vectors are the similar to
Eqs. (34), (35) and (36)
where 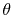 and
and 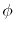 are the spherical coordinate
components of
are the spherical coordinate
components of 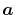 .
.
We come to the final equation, the derivatives of 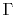 terms,
terms,
![$\displaystyle \frac{\partial}{\partial a} \Gamma^\ell_{\lambda \lambda'}(r, ) =...
...{dz} j_{\lambda'}(z) \right) \right\vert _{z = ka} {\tilde f}_\ell(k) \right] .$](img341.png) |
(A.3) |
As derived here, all the components are derived analytically,
without using any numerical differentiation.
In Eq. (30), there are terms proportional to 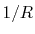 , which
diverge as
, which
diverge as 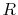 approaches to zero.
In fact,
approaches to zero.
In fact, 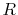 can be a near-zero values when, for example, atoms are
on a square lattice and the orbitals
can be a near-zero values when, for example, atoms are
on a square lattice and the orbitals 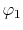 and
and 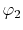 are
located at each end of a diagonal of the square, and
are
located at each end of a diagonal of the square, and 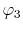 and
and 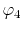 are at each end of the other diagonal.
To avoid such numerical problem, we impose a lower limit on
are at each end of the other diagonal.
To avoid such numerical problem, we impose a lower limit on 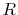 as follows:
as follows:
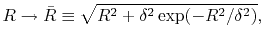 |
(A.4) |
where
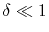 .
The same problem may arise for the derivative of
.
The same problem may arise for the derivative of 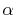 terms
(A2).
However, we do not need to consider the case when
terms
(A2).
However, we do not need to consider the case when 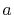 is close to zero.
This is because, in such case, the two orbitals are located on a same
atom and thus the derivative of the overlap function (A1)
should be always zero.
Here, we assume that all the orbitals are located on the atoms.
Note that the derivatives are not taken with respect to the orbital
centers but to the atomic positions.
is close to zero.
This is because, in such case, the two orbitals are located on a same
atom and thus the derivative of the overlap function (A1)
should be always zero.
Here, we assume that all the orbitals are located on the atoms.
Note that the derivatives are not taken with respect to the orbital
centers but to the atomic positions.
-
- [1]
A. D. Becke, J. Chem. Phys. 98, 1372 (1993).
- [2]
A. D. Becke, J. Chem. Phys. 98, 5648 (1993).
- [3]
P. J. Stephens, F. J. Devlin, C. F. Chabalowski, and M. J. Frisch, J. Phys. Chem. 98, 11623 (1994).
- [4]
C. Adamo and V. Barone, J. Chem. Phys. 110, 6158 (1999).
- [5]
P. Mori-Sánchez, A. J. Cohen, and W. Yang, Phys. Rev. Lett. 100, 146401 (2008).
- [6]
J. Heyd, G. E. Scuseria, and M. Ernzerhof, J. Chem. Phys. 118, 8207 (2003).
- [7]
J. Heyd and G. E. Scuseria, J. Chem. Phys. 121, 1187 (2004).
- [8]
I. Shavitt and M. Karplus, J. Chem. Phys. 36, 550 (1962).
- [9]
H. Taketa, S. Huzinaga, and K. O-ohata, J. Phys. Soc. Jpn 21, 2313 (1966).
- [10]
J. F. Rico, R. López, I. Ema, and G. Ramírez, J. Comp. Chem. 25, 1987 (2004).
- [11]
A. S. Torralba et al., J. Phys.: Cond. Mat. 20, 294206 (2008).
- [12]
J. M. Soler et al., J. Phys.: Cond. Mat. 14, 2745 (2002).
- [13]
T. Ozaki and H. Kino, Phys. Rev. B 69, 195113 (2004).
- [14]
T. Ozaki and H. Kino, Phys. Rev. B 72, 045121 (2005).
- [15]
T. Ozaki, Phys. Rev. B 74, 245101 (2006).
- [16]
J. D. Talman, Int. J. Quantum Chem. 93, 72 (2003).
- [17]
P.-O. Löwdin, Adv. Phys. 5, 1 (1056).
- [18]
A. E. Siegman, Opt. Lett. 1, 13 (1977).
- [19]
J. D. Talman, J. Comput. Phys. 29, 35 (1978).
- [20]
D. Lemoine, J. Chem. Phys. 101, 3936 (1994).
- [21]
O. A. Sharafeddin, H. F. Bowen, D. J. Kouri, and D. K. Hoffman, J. Comput. Phys. 100, 294 (1992).
- [22]
For example, in the discrete Bessel transform [20], an
interpolation process is necessary because the sampling points vary for
transforms of different orders. While, in the asymptotic expansion method
[21], high-order trasnforms are quite unstable due to the
factor inversely propotional to the
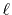 -th order of the variable where
-th order of the variable where
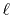 is the order of transform.
is the order of transform.
- [23]
J. D. Talman, Int. J. Quantum Chem. 107, 1578 (2007).
- [24]
http://www.openmx-square.org/.
This document was generated using the
LaTeX2HTML translator Version 2002-2-1 (1.71)
Copyright © 1993, 1994, 1995, 1996,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999,
Ross Moore,
Mathematics Department, Macquarie University, Sydney.
TOYODA Masayuki
2009-09-18
![]() density functional calculations.
Additional mathematical derivations are also presented
including the analytic derivatives of the integrals with
respect to atomic positions and spatial damping
of the Coulomb interaction due to the screening effect.
In the numerical test for a simple molecule, the convergence
up to
density functional calculations.
Additional mathematical derivations are also presented
including the analytic derivatives of the integrals with
respect to atomic positions and spatial damping
of the Coulomb interaction due to the screening effect.
In the numerical test for a simple molecule, the convergence
up to ![]() Hartree in energy is successfully
obtained with a feasible cost of computation.
Hartree in energy is successfully
obtained with a feasible cost of computation.
![]() DFT calculation codes, such as
CONQUEST [11], SIESTA [12]
and OpenMX [13,14,15], the strictly
localized pseudo-atomic orbital (PAO) basis sets are commonly
used since the real space sparsity of the resultant Hamiltonian
and overlap matrices enables us to combine the scheme with
various
DFT calculation codes, such as
CONQUEST [11], SIESTA [12]
and OpenMX [13,14,15], the strictly
localized pseudo-atomic orbital (PAO) basis sets are commonly
used since the real space sparsity of the resultant Hamiltonian
and overlap matrices enables us to combine the scheme with
various ![]() methods and to parallelize the computation by the
domain decomposition in real space.
Therefore, toward the implementation of the hybrid functionals
or any other methods which utilizes the Fock exchange in the
methods and to parallelize the computation by the
domain decomposition in real space.
Therefore, toward the implementation of the hybrid functionals
or any other methods which utilizes the Fock exchange in the
![]() DFT calculations, an effective numerical method is
required to evaluate the Fock exchange with using the non-analytic
PAO basis functions.
DFT calculations, an effective numerical method is
required to evaluate the Fock exchange with using the non-analytic
PAO basis functions.
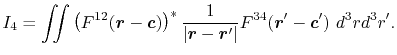
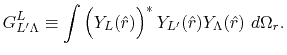
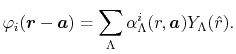
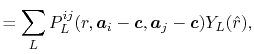
![]() -functions
are calculated through Eqs. (13) and (14).
From those
-functions
are calculated through Eqs. (13) and (14).
From those ![]() -functions, the overlap coefficients
Eq. (17) and the transformed ones
Eq. (18) are obtained.
Finally, the integral Eq. (9) is calculated by summing
up the radial integrals Eq. (10).
-functions, the overlap coefficients
Eq. (17) and the transformed ones
Eq. (18) are obtained.
Finally, the integral Eq. (9) is calculated by summing
up the radial integrals Eq. (10).
![]() and
and ![]() are changed
to their logarithms,
are changed
to their logarithms,
![]() is the Fourier transformed
spherical Bessel function:
is the Fourier transformed
spherical Bessel function:
![]() and
and ![]() , and then back-transformed with the same order.
In the transformed function (the upper middle panel), the oscillating
error appears in the small-
, and then back-transformed with the same order.
In the transformed function (the upper middle panel), the oscillating
error appears in the small-![]() region.
After the back-and-forth transform (the upper right-hand panel), the
accumulation of error is observed.
Often, the error approaches quickly to infinity and the computation
crashes.
region.
After the back-and-forth transform (the upper right-hand panel), the
accumulation of error is observed.
Often, the error approaches quickly to infinity and the computation
crashes.
![]() region, we perform the
integration of Eq. (20) for some selected
region, we perform the
integration of Eq. (20) for some selected ![]() -points
between 0 and
-points
between 0 and ![]() by using the straightforward trapezoidal method,
where
by using the straightforward trapezoidal method,
where ![]() is smaller than the smallest
is smaller than the smallest ![]() -points used in the
final integration Eq. (10) so that the effect of the
correction can be negligible, but the numerical breakdown can be
avoided.
By a linear interpolation between the selected
-points used in the
final integration Eq. (10) so that the effect of the
correction can be negligible, but the numerical breakdown can be
avoided.
By a linear interpolation between the selected ![]() -points,
we obtain another transformed function
-points,
we obtain another transformed function
![]() ,
in addition to
,
in addition to
![]() .
Then we replace
.
Then we replace
![]() with
with
![]() for
for ![]() as follows:
as follows:
![\includegraphics[width=0.9\textwidth]{fsbt.eps}](fig1.png)
![]() can be calculated immediately since
all the differentiations in Eqs. (30) and (31)
are taken for the analytic functions.
As shown in the appendix, the differentiations of the
overlap functions in Eqs. (32) and (33) can also be performed completely analytically.
Note that the differentiations are taken only for
can be calculated immediately since
all the differentiations in Eqs. (30) and (31)
are taken for the analytic functions.
As shown in the appendix, the differentiations of the
overlap functions in Eqs. (32) and (33) can also be performed completely analytically.
Note that the differentiations are taken only for ![]() and
and
![]() because the others can also be obtained via the
following sum rule:
because the others can also be obtained via the
following sum rule:
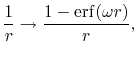
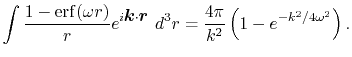
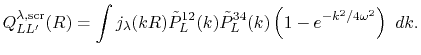
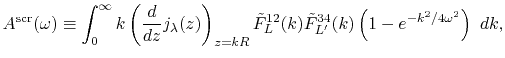
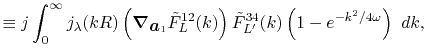
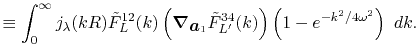
![]() has also
a significant effect on the convergence speed.
In general,
has also
a significant effect on the convergence speed.
In general, ![]() is an orbital-dependent value.
Therefore, since
is an orbital-dependent value.
Therefore, since ![]() -functions Eqs. (13)
and (14) depend on
-functions Eqs. (13)
and (14) depend on ![]() (note that what we
actually need is the terms in the right-hand side of Eq.
(17)), one needs to calculate those coefficients
of which the number is equivalent to that of neighboring orbitals.
Here, we offer a suggestion that the computation cost may be
reduced by choosing
(note that what we
actually need is the terms in the right-hand side of Eq.
(17)), one needs to calculate those coefficients
of which the number is equivalent to that of neighboring orbitals.
Here, we offer a suggestion that the computation cost may be
reduced by choosing ![]() at the middle of the two orbital centers,
at the middle of the two orbital centers,
![]() Hartree.
The difference from the comparison values is large for
Hartree.
The difference from the comparison values is large for ![]() and
and
![]() because the C-
because the C-![]() inner-shell orbital is involved.
In general, the small spatial extent of such the inner-shell orbitals
makes the convergence slower.
This, however, would not have to be considered so seriously in the
actual calculations if the contribution of the inner-shell
electrons are included in the pseudopotentials.
inner-shell orbital is involved.
In general, the small spatial extent of such the inner-shell orbitals
makes the convergence slower.
This, however, would not have to be considered so seriously in the
actual calculations if the contribution of the inner-shell
electrons are included in the pseudopotentials.
![]() ,
, ![]() and
and
![]() are used.
The comparison values are also calculated by using the present
method with the enhanced parameters
are used.
The comparison values are also calculated by using the present
method with the enhanced parameters
![]() and
and ![]() .
As well as the analytic functions such as GTO and STO basis sets,
even for the strictly localized PAO basis set, it is confirmed that
the convergence up to
.
As well as the analytic functions such as GTO and STO basis sets,
even for the strictly localized PAO basis set, it is confirmed that
the convergence up to ![]() Hartree is obtained with
Hartree is obtained with
![]() .
.
![]() can also be used for
can also be used for ![]() etc.
Therefore, the computation efficiency in total can
be significantly enhanced as the system size becomes
larger.
etc.
Therefore, the computation efficiency in total can
be significantly enhanced as the system size becomes
larger.
![]() terms,
terms,
![$\displaystyle \frac{\partial}{\partial a} \Gamma^\ell_{\lambda \lambda'}(r, ) =...
...{dz} j_{\lambda'}(z) \right) \right\vert _{z = ka} {\tilde f}_\ell(k) \right] .$](img341.png)
![]() , which
diverge as
, which
diverge as ![]() approaches to zero.
In fact,
approaches to zero.
In fact, ![]() can be a near-zero values when, for example, atoms are
on a square lattice and the orbitals
can be a near-zero values when, for example, atoms are
on a square lattice and the orbitals ![]() and
and ![]() are
located at each end of a diagonal of the square, and
are
located at each end of a diagonal of the square, and ![]() and
and ![]() are at each end of the other diagonal.
To avoid such numerical problem, we impose a lower limit on
are at each end of the other diagonal.
To avoid such numerical problem, we impose a lower limit on ![]() as follows:
as follows: